Натрупаната нормално разпределение функция - енциклопедия на икономиката
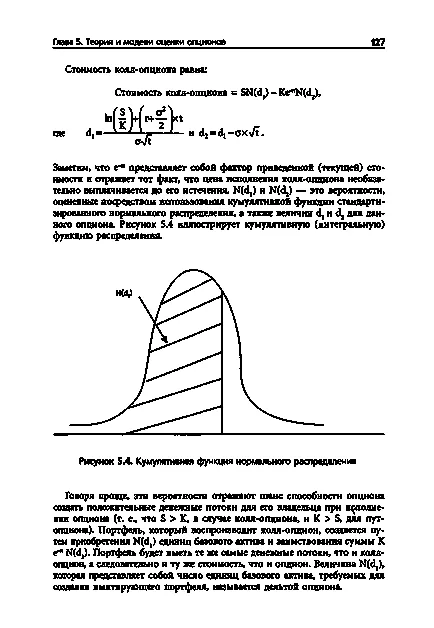
Фигура 5.4. Натрупаната функция нормално разпределение
Един от най-интересните резултати от модел на ценообразуване на опции - риск неутрален вероятност от неизпълнение, които могат да бъдат получени за фирмата. Моделът на Black-Scholes може да се изчисли въз основа на стойността на кумулативното нормално разпределение функцията N (d2), която е неутрална вероятността на риска над над K S (S> С). Моделите на ценообразуване на опции, тази стойност е вероятно да надхвърли стойността на активите на фирмата над номиналната стойност на дълга. [C.1096]
Кумулативна нормално разпределение функция 127 купони 15 [c.1301]
N (г) кумулативен нормално разпределение функция срещу нестабилността на (годишна стандартно отклонение) [c.407]
кумулативната функция на нормално разпределение може да се сближи със следния полином (полином). На първо място, да се изчисли стойността на х. Y и Z. За N (г) г [c.407]
Следващата стъпка в таблиците са стойностите на стандартизиран кумулативно нормално вероятностно разпределение на точки 0.6 и 0.4. Алтернативен метод за изчисляване на кумулативните стойности на стандартното нормално функцията на вероятностно разпределение е да се намери полином, който е обяснено в Sec. 8. [c.480]
При конструирането на кумулативен регресия форма F (х) на функцията на разпределение не е основна природа, въпреки че е известно [90], с оглед използва в този случай метода на най-малките квадрати оценки получава най-добре нормално право разпределение. [C.155]
Имайте предвид, че е стайна температура е фактор дал (ток) стойност и отразява факта, че цената на упражняване на кол опция, задължително платени преди изтичането му. N (DJ) и N (d2) - вероятността се оценява чрез използване на стандартизиран кумулативен нормалната функция на разпределение. и г и D2 стойности за тази опция. Фигура 5.4 илюстрира кумулативния (с натрупване) функцията на разпределение. [C.127]
Taylor [159] изучава проблемите на икономическа обосновка списъци кумулативни суми стойност на проба от нормално разпределение с известно вариране на качествения рейтинг. Той се основава на факта, че контролната карта кумулативни суми са предназначени за процес на откриване промяна точка на образуване на предварително определено качество мярка на предположението, че разстройство настъпва внезапно с известна компенсира параметър. Очаквано време на безредици предполага известна. Процесът е спрян, за да реши проблема. Ако сигналът не е разстройството е погрешно, това отнема повече време, за да се намери причината за проблема и да го оправя. функция приблизителната стойност на базата на следните предположения [c.137]
От стандартни таблици кумулативната функция на разпределение на случайна променлива нормално разпределение намираме [c.165]
N (DJ) Н Н (d2) - кумулативното нормално вероятност по-точно, кумулативен нормално вероятностно разпределение функцията на стойностите на плътност или кумулативни вероятност за разпространение RMS съответно D1 и D2 на; като се вземат предвид стандартното отклонение на акциите за достатъчно дълъг период от време (а). [C.135]
N () = кумулативна нормалната функция вероятностно разпределение, определен от уравнението (3.21). [C.156]
N () = кумулативна нормалната функция вероятностно разпределение, [c.237]
NORMDIST () функция изчислява кумулативен нормалното разпределение и резултатът е число между нула и единица. Р1 () функция поддържа математическа константа "п". LN () е естествен логаритъм. EXP () - аргументи за експонента, а SQRT () пресмята корен квадратен. [C.210]
N (г) = Площ под кривата на стандартната нормалното разпределение или вероятност, че нормално разпределение със средна стойност 0 и стандартно отклонение. равно на 1, резултатът ще бъде съответно по-малко дл и D2 (или друга дефиниция на функция кумулативен нормална вероятност плътност). Изчисляване N (г) от Пример ел следва функция - "NORMRASPR (г 0 л Н THHa)". [C.65]