Нахранете електрически вектор поле
Vector поток $ \ overrightarrow \ $ повърхност чрез $ S $ нарича алгебрична стойност $ _A $, която се определя, както следва:
Знакът на потока зависи от избора на посоката на нормалата към началното района $ DS $.
Елементен поток интензитет вектор
Позовавайки се на електрическото поле. интензивност модул е равен на броя на силови линии, които се пресичат повърхността, която е равна на един, повърхността трябва да е перпендикулярна на линиите на полето в дадено място. Броят на силови линии, които преминават по-горе име повърхност, наречена вектора на потока на напрежение. Ако подчертае елементарен повърхностна площ (DS), да се конструира нормална към този сайт $ \ overrightarrow $, където ъгъла между нормалата и посока вектор количество $ \ алфа $ на, елементарния поток на интензивност вектор ($ $ dF_E) могат да бъдат написани като:
\ [DF_E = EdScos \ алфа = \ overrightarrow \ cdot г \ overrightarrow \ \ наляво (2 \ полето), \]
В уравнение (3) $ \ overrightarrow $ единица нормално да сайт $ $ DS.
Ако ние считаме всеки - или всяка повърхност $ S $, можем да запишем, че потока на интензитета на вектор ($ $ F_E) в съответствие с дефиницията на вектора (1) Скорост на потока:
\ [F_E = \ Int \ limits_S \ cdot г \ overrightarrow> \ \ \ наляво (4 \ дясно). \]
Посоката на нормалата
Както и в общия случай, вектора на потока на алгебрични стойност. знак на потока зависи от конфигурацията на терена и посоката на вектора - нормалната $ \ overrightarrow $. Посока нормално условно. Може да се каже, че интеграл в уравнение (4) представлява обща мощност източник вектор $ \ $ overrightarrow, с които са таксите вътре в обема, което ограничава повърхност $ S $.
Смята се, че когато се работи с плътна повърхност, на нормалната посока е положителен навън. Потока интензитет вектор в случай на затворена повърхност се записва с линия неразделна заедно затворена повърхност:
\ [F_E = \ Съвместният \ limits_S \ cdot г \ overrightarrow> \ \ \ наляво (5 \ дясно). \]
Цел: електрически интензитет на поле се определя по формулата в декартови координати:
където $ \ overrightarrow \ \ $ overrightarrow - единичен вектор на вола и OY оси. Намерете поток на вектор $ \ $ overrightarrow на чрез сферична повърхност, ако неговия радиус е равен на R $ $, и нейния център е в основата.
Като основа за решаването на използване на определението на поток вектора на напрежение, а именно:
\ [F_E = \ Int \ limits_S \ cdot г \ overrightarrow> \ \ \ наляво (1.1 \ полето), \ \]
където $ г \ overrightarrow = \ overrightarrowdS $, $ DS- $ елементарна повърхност пространство сфера, $ \ overrightarrow $ - нормално за тази област.
Ние напиши експресията на нормалата към повърхността на сферата, под формата на:
Ние замести (1.2) в (1.1), като се използва израза за напрегнатостта на полето на условията на проблема, ние откриваме интегралната, като по този начин, когато продуктът в подинтегрален, смятат, че $ \ overrightarrow, \ overrightarrow \ overrightarrow $ - правоъгълни единичен вектор.
Цел: Определяне вектор поток през напрежение сферична повърхност, ако е в рамките на две точкови такси $ + q_1 $ и $ $ _2.
Като основа за решение могат да вземат за формула поток интензивност вектор като:
\ [F_E = \ overrightarrow \ cdot S \ overrightarrow = ЕСКО \ а \ \ наляво (2.1 \ полето), \]
където $ \ алфа $ - ъгъла между нормалата към повърхността чрез който търси и поточно интензитет вектор. област точка заряд има сферична симетрия (Фиг.1). Следователно, векторът и напрегнатост на полето на вектора - нормално са codirectional ($ защото \ алфа == $ 1). Фиг. 1 показва поле на положителен заряд.
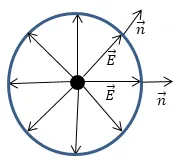
Получената интензивността на полето може да бъде получена в съответствие с принципа на суперпозиция от полетата на двете такси, с героите.
Пишем израз в полето модул, което създава първото зареждане:
За втора такса:
Ние намираме модула на получените напрежение, тъй като положителен заряд - източник на терена и отрицателната - областта поток, т.е. посока, обратна на полетата:
Ако погледнем за потока през сфера, която има радиус R, след израза (2.4) е под формата:
Площ на сфера (S) е равна на предварително определен радиус:
В този случай, замени изразите (2.6) и (2.5) до (2.1), ние се отбележи, че $ защото \ алфа == $ 1, получаваме: