Начин на локуси в решаването на проблемите на сградата

Решаване на проблеми с HMT е както следва:

А) проблем е формулиран така, че нейното решение се свежда до намиране на парчета, които не отговаря на едно или повече условия.

Б) Ако състоянието е един, разтворът на проблема ще бъде съответно място. В случай, че на няколко условия, а след това, хвърляйки един от тях, които получаваме нов проблем, чието решаване ще бъде една или повече от HMT. Това място е известен и лесно конструирани.

Б) След това, като се има предвид състоянието на излязло от употреба и изхвърляне на всяко друго състояние, получи нов локус.

Г) точки са решения на проблеми (ᴛ.ᴇ. напълно удовлетворява своите ИТ условия ??) трябва да принадлежат към двете първи и втори локус. Така че, те трябва да принадлежи на пресичането им.

Задачата има решение или не въз основа на факта, дали или не на мястото, имат общи точки. Той ще има най-много решения, тъй като има пресечни точки.

Пример 4.Postroit кръг допирателна на кръга в точка В, и тази линия MN. (Фиг. 5).

Анализ. Да предположим, че проблемът е решен, ᴛ.ᴇ. окръжност с център О1 удовлетворява условията на проблем, ᴛ.ᴇ. допирателна към окръжност с център О точка и по отношение на правата линия MN. След това центровете на желаните кръгове лежат на OB на линия (HMT номер 6). Като от В допирателна към двата кръга до пресечната точка с MN в точка R, ние получаваме че желаният ъгъл на окръжността, вписан в NKV. Следователно, тя

център се намира на ъглополовящата на ъгъла (HMT № 11); ъглополовящи съседен ъгъл, ние получаваме второто решение.

Сграда. Чрез точки Б и Г държи права линия. В допълнително чрез допирателна към предварително определен обиколката. Качваме се на ъглите и Мака BKN. Изграждане на ъглополовящата на ъгъла. Тяхната пресичане с OB линия получат желаните центровете на кръгове - O1 и O2. Изграждане на окръжност с център в O1 O1 в радиус и окръжност с център в O2 O2 радиус Б.

Това следва от строителството.

Изследване. Броят на разтвори зависи от относителното положение на кръг О и линията MN. Има три случая.

1) Директно MN още няма общи точки с кръга. В този случай, проблемът е, както вече сме обсъждали, двата разтвора. (Демонтирайте собствен случай, когато MN # 9553; IN).

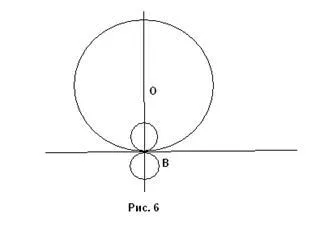
2) Директна MN допирателна към окръжността. Ако възникне контакт в точка В, тогава проблемът е безкрайно много решения (фиг. 6). Всички центровете на кръговете се търсят по линията OB.

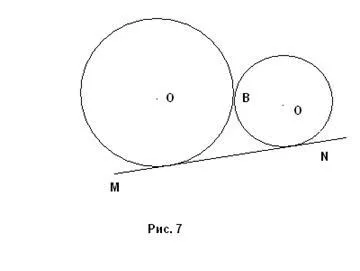
Ако точка Б не е една и съща точка на допиране. Тогава проблемът е един разтвор (фиг. 7).

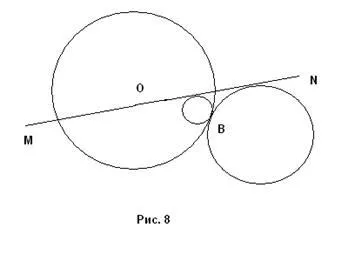
3) Директен MN пресича този кръг. Ако една от точките на пресичане съвпада с точка В, след това не съществуват решения. В случай, MN не преминава през точка В, двата разтвора (фиг. 8).

Пример 5.Postroit триъгълник и основата, височина ха и страничната б.

Анализ. Да приемем, че триъгълник ABC е конструирана и има Слънцето = а, СА = б и vysota͵ понижава от върха А, е ха. Тогава множеството от слънце ?? бивши върхове на триъгълници с

основа и височина ха ще лежи по две линии, успоредни на слънцето и на разстояние от нея на разстояние ха (HMT № 10).

Освен това, тъй като CA = б, след точка А се намира на определено разстояние от точка С, което означава, че се намира на окръжност с радиус б центриран в точка С (HMT № 1). Следователно, точка А е пресичане на два HMT и следователно се засича.

Сграда. На произволен ред Mn от произволна точка в отлагане на сегмента BC = а. От всяка точка на линията MN изготвили ^ MN FK и FK K от двете страни съкращават сегменти КТ и KE равен ха. След T и E изпълнява директно п и т, перпендикулярна на ТЕ. От гледна С задържане кръг с радиус б.

Пресечната точка на този прав периферен m и п е желаната точка А. го свързва с точки В и С на триъгълник ABC - желания.

Доказателство. В триъгълника ABC VS = база от строителството, връх А се отстранява от дъното на разстояние ха. странична страна Ас = б.

Изследване. Ако б> ха. имаме четири решения. защото радиуса на окръжност пресича линии m и п в четири точки.

Ако б = ха. получаваме две решения, като направо пит ще докосне обиколката.

Ако б

виж също

Посрещане на предизвикателствата на метод HMT е както следва: А) проблемът е формулиран така, че нейното решение се свежда до намиране на парчета, които не отговаря на едно или повече условия. Б) Ако състоянието е един, разтворът на проблема ще бъде съответно място. Ако условията. [Прочети още].