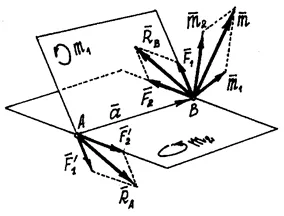
Момент на сила за център (или точката)

Опитът показва, че под действието на силата на твърдото тяло може заедно с постъпателното движение се върти около даден център. Ротационна сила ефект се характеризира със своята мигове-хау.

Помислете сила. свързан в точка А твърдо тяло (фиг. 11). Да приемем, че силата, има тенденция да се върти тялото около центъра О. перпендикулярна часа. спадна от центъра на О по линията на действие сила. се нарича по-рамо в относителната сила на центъра О. Тъй като точката на прилагане на силата може да бъде произволно завой Schat по линията на действие, е очевидно, че ефектът на ротационните сили ще зависи от: 1) на модула на сила F и раменете Н; 2) от поло равнина въртене zheniya ОАВ. минаваща през центъра О и siluF; 3) на посоката на въртене на тази равнина.

Ние се ограничаваме само до разглеждане на силите, докато системите, които се намират в една и съща равнина. В този случай равнината на въртене на всички сили се среща често и не се нуждаят от допълнителни задачи.

След това, за количествено измерване на въртене ефект може да се въведе следната понятието сила момент: момент на сила за център O е определена да бъде равна на заснети с подходящ знак за силите на продукт модул до раменете.

Момент на сила за център О ще бъде означен сим вол m0 (F). Ето защо,

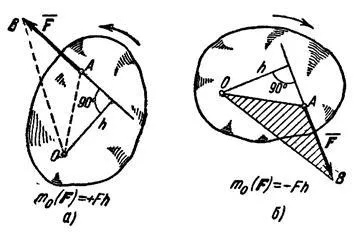
В бъдеще, ние сме съгласни, че времето е положителен, ако силата се стреми да се превърне в тялото около център O обратно на часовниковата стрелка, както и знака минус - ако по часовниковата стрелка. Така че, за силата. показан на Фигура 20, както добре. момент за център О е положителен, и за силата е показано на фигура 20 б. - знак E конус.

Обърнете внимание на следното свойства сила момента:

1) на въртящия момент не се променя, когато се движат точка прилагане на сила по линията на действие.

2) В момента на сила за център о е нула само когато силата е нула или когато линията на действие сила преминава през центъра О (рамото е равна на нула).

3) Въртящ момент числено изразени удвоява площ Thr-гон BAW (Фиг. 20b)

Този резултат идва от факта, че

Смятан за да се определи моментът на силата е подходящ само за плосък система сили.

Пиер Varignon теорема на полученото в момента.

Пиер Varignon докажем следната теорема. Понастоящем Получената равнина система от схождащи сили за всеки център-алгебра е алгебрично сума на моментите на силите отношение спрямо същия център.

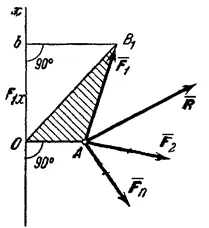
Помислете система сили. схождащи в точка А (Фигура 12). Вземете произволна център О и изготвя чрез оста х. перпендикулярна на правата линия ОА; положителната посока на оста х се подбира така, че знакът на проекцията на всяка от силите на тази ос съвпада с тази на своя момент около центъра О.

За да се докаже теоремата намираме съответните моменти на изразяване m0 (), m0 (), .... Съгласно формулата. Но, както е видно от фигурата, където F1x - проекция на сила върху оста х; следва последователност

.

По същия начин, изчислена моменти на всички други сили.

Означаваме получените сили. чрез. къде. След това, от теоремата на проекция сборът на силите на предния мост, ние получаваме. Увеличаването двете страни на това уравнение с ОА. намерите:

.

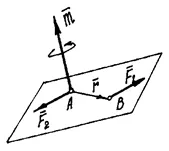
Чифт сили (или две) са двете сили, които са равни по VE-лик, паралелно и насочени в противоположни посоки (Фигура 13). И това е очевидно.

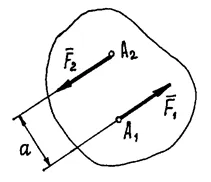
Въпреки факта, че сумата на силите е нула, тези сили не са балансирани. Под действието на тези сили, двойката на силите, тялото ще започне да се върти. И въртене ефект ще се определя от инерцията на двойката:

.

а разстоянието между линиите на силите нарича рамо чифт.

Ако двойката се превръща в тялото на часовниковата стрелка момент се счита за положителен (както на фигура 13), ако по часовниковата стрелка - отрицателна.

За да двойка посочено време и равнината, в която се появява въртене, тя е представена като вектор.

Момент вектор двойка е насочен перпендикулярно на равнината, в която двойката е разположена по такъв начин, че ако погледнете от до, вижте въртенето на тялото обратно на часовниковата стрелка (фиг. 14).

Лесно е да се докаже, че вектор MO-среда двойката - е вектор на вектора на продукта (фиг 14.). И над ние наблюдаваме, че тя е равна на вектор момента на сила, за точка А. Точката на прилагане на втората сила:

.

На приложения точка векторни Bu деца обсъдени по-долу. Макар да го прикачите към точка А.

1) двойка на издатък на всяка ос е нула. Това следва от определението за чифт сили.

2) Намираме количеството оставяйки няколко моменти на сили, по отношение на някои точка O (Фигура 15).

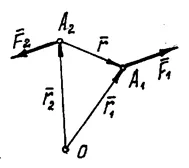
Показване радиуси вектори на точките А1 и А2 и вектора. свързваща тези точки. След това към момента на двоица сили спрямо точка О

.

Момент на няколко сила по отношение на всяка точка е равна на времето на тази двойка.

От това следва, че, на първо място, където ще открием точка O и второ, когато не са се заселили тази двойка в организма и как тя не е била завъртяна в неговата равнина, и влиянието му върху тялото няма да бъде същият. От момента на силите, които съставят двойката, в тези случаи е една и съща, равно-ъглов момент на тази двойка.

Поради това е възможно да се формулира още две свойства.

3) двойка може да се движи вътре в тялото на равнината на действие и да се премести в друга паралелна равнина.

4) Тъй като ефектът върху организма на силите, които съставят двойката, се определя само от инерцията си, продуктът на една от силите на рамото, след което двойката може да се променя силата и рамото, но така, че инерцията на двойката е останала същата. Например, когато силите F1 = F2 = 5 Н рамото и = 4 см точка двойки m = 20 Н # 8729; вж. Група може да се направи равно на 2 N и = рамо 10 см. В този момент остава непроменена и ефекта от 20 NCM двойки на тялото на menitsya.

Всички тези свойства могат да се комбинират и, като следствие, смятате ли,-води, която съответства на същия вектор на момента, независимо къде се намират по тялото имат равен ефект върху него. Това означава, че тези двойки са еквивалентни.

На тази основа, изчислено на двойка вериги е изобразена като дъга със стрелка показва посоката на въртене, и следващия път запис стойност М (фигура 15.1). Или, ако пространствената структура, по-само доказва вектор момента на двойката. И миг вектор двойка може да се прилага за всяка точка от тялото. Следователно момент вектор двойка - без вектор. Този опростен образ обосновано от факта, че двойката на въртящия момент сили се характеризира, а не от позицията си в самолета. Но ако трябва да се определи не външни сили и вътрешно в различни секции на елемента, както се прави в силата на материали, важно е знак и място на подаване на заявлението чифт сили.

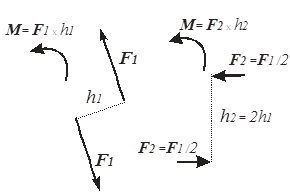
Фигура 15.1. Еквивалентно сила двойка

И още един допълнителен коментар. От момента на чифт РА вени инерция вектор на една от силите, по отношение на нейната точка на прилагане на втората сила, момента на двойката сили по отношение на Z-оста - е проекция на ъгловите скорост векторни двойки на тази ос:

,

където - ъгълът между вектора и оста Z.

Да се ​​даде два чифта с М1 и М2 моменти. отново подредени в пресичащи се равнини (фигура 16).

Ние правим рамото имат еднакви чифта равни а = AB. Тогава модулите на силите, които са първата двойка трябва да бъде равна, и които са втори чифт :.

Тези двойки са показани на Фигура 16, където. И те се намират в самолетите си, така че раменете двойки съвпадат с правата линия AB Перес-cheniya равнини.