Методът за създаване и решаване на Кирхоф уравнения
Да предположим, че в една верига, съдържащ "м" клони към "п" възли са всички посочени елементи и конфигурация като търсените - течения в клоновете. Броят на неизвестни в този случай е броят на клонове.
Ние очертае изчисляването на път.
1). Изборът произволна положителна посока на токовете в клоновете (което е в клоните на източник на напрежение на прав ток посока EMF).
2). Се равнява на закон за 1-ви Кирхоф. Може би рисуване "N" уравнения на формата.
Лесно е да се забележи, че всеки ток ще влезе две уравнения с противоположни знаци. Следователно, сумата от уравнения е идентично равно на нула, т.е. един от уравнения, получени от останалите N-1. Вследствие на това на практика на 1-ви Кирхоф трябва да се направи N - 1 независими уравнения.
3). Определяне на изчезнали "м" неизвестните токове уравнения да бъдат написани от втория закон на Кирхоф. Те трябва да имат m - (N - 1) = m - п + 1.
Ако всички клонове прилагат закона на Ом, получаваме "М" уравнения на формата :. при което - напрежението между възли и и р. ЕК. Ik - едн източник и тока в клон к- тия насочено от възел до възел стр. R - резистентност към втората част. По-удобно влизане :.
Закон уравнения на Ом са "М" неизвестни течения Ик и N-1 неизвестни потенциали (потенциала на един възел е настроен на нула). Ако изключим тези неизвестни потенциали остават м - н + 1
уравнения, свързани източника на ЕМП с напрежение върху резистора, т.е.. д. уравнението на правото на втория Кирхоф. За да бъде независим от уравнението, е необходимо, че всеки запис е най-малко един нов клон. Почти удобно да пиша уравнения за схеми, които нямат клонове вътре, т. Е. За клетките.
4). Броят на необходимите уравнения на 1-ви и 2-ри законите Кирхоф може лесно да бъде инсталиран на веригата на колоната. За това е дърво на графиката. Преди това тя установява, че броят на клонове в дървото на графиката е точно равна на п - 1,
т. е., равен на броя на необходимите и достатъчни уравнения 1-ви закон на Кирхоф. Броят на необходимите и достатъчни уравнения 2-ри Кирхоф право м - н + 1 е броят на комуникационни клонове.
5). При изчисляване вериги често определят захранващи източници и приемници на енергия. Имайте предвид, че тя трябва да бъде на закона за запазване на енергията, в резултат на което
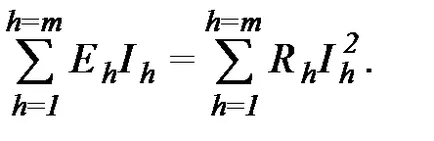
В лявата част на съвпадението на посоки Eh и час продукта е положително, и отрицателно, когато nesovpadenii-.
6). Ако има токов кръг източник, те трябва да бъдат взети под внимание при писане на уравнения право 1-ви Кирхоф. За да ги даде енергия се отчита в лявата страна на уравнението на властта баланс.
7). Ако токът се определя отрицателен, в обратната посока на неговата действителна приета в началото на изчислението.
Метод линия течения (клетки).
Той е един от основните методи за сложни схеми за изчисление. Тя се състои в това, че вместо да токовете в клоните се определя въз основа на закона на втората Кирхоф т.нар контурни токове. Така isklyuchayutsyauravneniya право 1-ви Кирхоф.
За независими кръга на втория закон на Кирхоф:
Ние премахване на сегашните местни клонове, не ги изразяват по отношение на външните токове
Получената система от уравнения, съдържа три неизвестни I1, I2, I3. чрез които може да се определя iI5 I4.
Формулите могат да бъдат написани веднъж чрез присвояване на всяка клетка на определен ток на контура, което съвпада с настоящите външни клоните. След това, във всяка клетка алгебричната сума на електродвижеща сила, равна на алгебричната сума на продуктите
а) контур ток на схема клетка в размер на устойчивост на;
б) бримкови токове всяка съседна клетка - от съпротивление съседни клонове.
Знакът е същият, както при писането на уравненията на правото на втория Кирхоф.
Общ вид на уравненията за "N" вериги, където Rnn - размера на устойчивост на п-ия клетката, RN2 - сума от клоновете на съпротива общи за н-ти и 2-ри вериги,
En - алгебричната сума от едн н-ия кръг.
Получената система може да бъде решен с помощта на детерминанти:
където
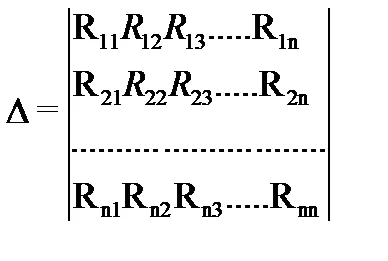
Ако веригата се състои от източник на ток, токът може да се вземе от всеки блокиращ клонове всеки отворен цикъл, допълването на клона с източник на ток в затворена. Спадът в напрежението се дължи на този ток съпротивление на веригата се взема под внимание заедно с пада на напрежение на бримкови течения.
Метод на възловите потенциали.
Този метод намалява броя на уравнения на уравнения Кирхоф чрез премахване на 2-ри закона. На диаграмата, ние сме като потенциала на точка "О" на нула.
Ние изразяваме токовете на всички клонове в непосредствена близост до възел "а" от закона на Ом:
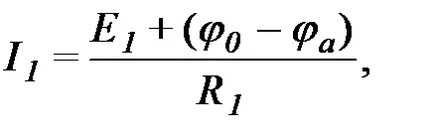
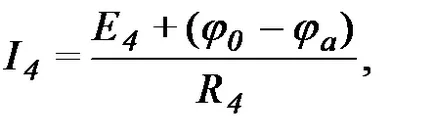

Въз основа на закона на 1-ви Кирхоф: т.е. ,
Подобна форма на уравнение може да бъде получена за една възлова точка "б", и за всеки възел в по-сложна схема.
Анализ на уравненията показва, че за всеки възел алгебричната сума от продукти на едн на проводимостта на свързаните отрасли е
а) на потенциала на този възел пъти сумата на стойностите на проводимостта на свързани клонове,
б) потенциал минус продукта от други възли, всяка умножена по сумата на проводимостта на клонове, свързващи възел с тази, за която е написано уравнението.
Ако електродвижещата сила е насочена към възела, след Ek Gk влиза в уравнение с "плюс" на обекта - на "минус".
източниците на ток трябва да се вземат предвид в лявата страна на уравнението с "плюс", ако те са насочени към възела. Общата форма на уравненията: където: G11 - сумата от проводимостта на клонове, свързани към първия възел, G12 - сумата от проводимостта на клонове, свързващи първия възел с втората.
Формулите са написани за (N - 1) възли и решени, например, като се използва детерминанти. Според получените възлови отрасли се определят от токове с помощта на закона на Ом.
наслагване метод (суперпозиция).
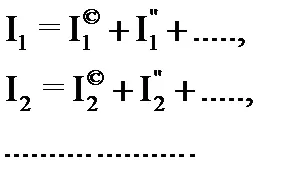
Решение на системата от линейни уравнения еднозначно определя течения.
Ако приемем, последователно в една и съща верига, която има само един едн под друго, равно на нула, то е възможно да се изчисли електродвижеща сила на всеки клон съответните токове, като уравнение:
Добавянето на срока на уравнения от термин, ние получаваме:
Получената система има уникално решение за неизвестен и т.н.
От сравнението на оригиналните уравнения и току-що получи от това следва, че решението трябва да бъде същото, т.е.
По този начин, всеки клон ток е равен на сумата от алгебрични частични токове, образуван от действието на всеки поотделно едн (наслагване принцип).
Това изчисление се основава на метода на наслагване верига.
Напрежението на част верига с R. на резистентност
т.е. суперпозиция принцип се прилага към стреса.
наслагване принцип важи и за източника на ток. В същото време останалата част от източниците на ток са изключени.
принципа на суперпозиция не се прилага за електрически - квадратно функции на токове и напрежения.
Превръщане на електрически вериги.
Различни трансформации се прилагат обикновено в комбинация с други методи за изчисление. В тази еквивалентна схема е определен, но изчисляване на токове е значително опростена.
Ако електродвижещата сила действа в комплекс клонове верига / р / едн в отсъствието на други причини в друг клон / L / ток Ил. същото електродвижещата сила, действаща в отсъствие на L разклонения на едн да накара първата / р / същия ток
Съгласно метода на бримкови токове:
От настоящата система в бранша, където L се определя от
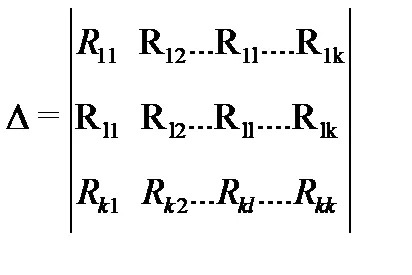
Общото съпротивление Rql и Rlq. равен, тъй като R12 = R21. R23 = R32 и т.н. Следователно, и се различава само по това, редовете са колоните .Sledovatelno принцип могат да се прилагат, например, за определяне на токовете в различни клонове на веригата в един едн.