Методи за решаване на нелинейни уравнения
Ключови думи: нелинейни уравнения, приложна математика, CAD на MathCAD, метод на Нютон, стъпка метод, методът на дихотомия.
Цел: Да се проучи методите за решаване на нелинейни уравнения с едно неизвестно и да ги тествате в експерименталната работа.
- Анализирайте специална литература и да се избере най-рационални начини за решаване на нелинейни уравнения, което позволява на дълбоко проучване и асимилира предмет за всички зрелостници.
- Да се разработи някои аспекти на методите за решаване на нелинейни уравнения с използването на ИКТ.
- Разгледайте методи за решаване на нелинейни уравнения:
- Метод на разполовяване
Да предположим, че искате да се реши нелинейно уравнение от вида на уравнението F (х) = 0. Ние също така да приемем, че ние сме зададен интервал търсене [x0, x1]. Изисква търсене интервал [а, Ь] на дължина часа, съдържащ първи корен на уравнението, от лявата граница на интервала на търсене.
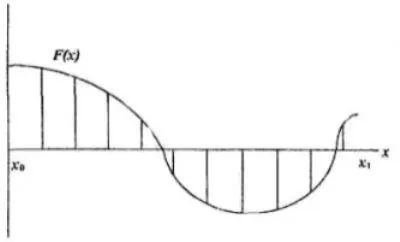
Фиг. Метод 1. стъпка
За да реши този проблем по няколко начина. Етап метод е най-простият на числени методи за решаване на неравенства, но за да се постигне висока точност необходимо да се намали значително етап, и значително увеличава изчисленията време. Алгоритъм за решаване на уравненията на използването на този метод се състои от два етапа.
На този етап на части, всяка от които съдържа само един корен на уравнението. Има няколко възможности за изпълнението на тази фаза:
- Заместник настройка, за да X (за предпочитане с някои доста фина стъпка) и да видим къде функцията променя знак. Ако функцията се променя знака, което означава, че районът между предишната и настоящата стойност на X е корен (ако функцията не променя характера на увеличение / намаление, може да се твърди, че в основата на този интервал един).
- Графичен метод. график строителство и оценка на какви интервали е един корен.
- Ние изследват свойствата на определена функция.
На този етап е дефинирано по-рано определен стойността на корена на уравнението. Обикновено този етап се използва итеративни методи. Например, методът на разполовяване (дихотомия) или метод на Нютон.
Метод разполовяване
достатъчно бърз и прост цифров метод за решаване на уравненията на базата на последователно свиване интервал, съдържащ уникален корен на F (х) = 0 до времето до предварително определена точност Е. Този метод обикновено се използва в разтвор на квадратно уравнение и уравнения на по-висока степен. Въпреки това, този метод има значителен недостатък - ако интервалът [а, Ь] съдържа повече от един корен, след това се използват не за да могат да се постигнат добри резултати.
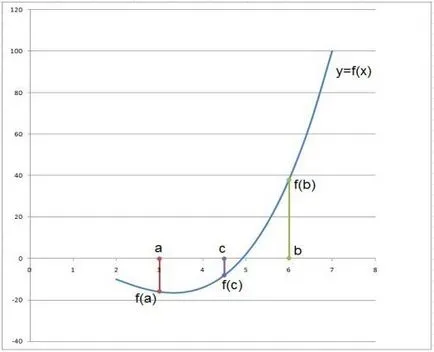
Фиг. 2. Метод съгласно дихотомия
Алгоритъмът на този метод е, както следва:
- идентифициране на нов сближаване на основата на X в средата на интервала [а, Ь]: X = (А + В) / 2.
- Виж, че стойностите на точките за една и х: F (а) и F (х).
- Проверка на състоянието F (а) * F (х) 0. По този начин, точка с x0 абцисата е избран. в която допирателната към крива у = F (X) в интервала [а, Ь] пресича Ox ос. За първи точка x0 е удобно да се избере един от краищата на сегмента.
Нека разгледаме алгоритъма на конкретен пример.
Да предположим, че са дадени нарастваща функция у = е (х) = х 2- 2 е непрекъсната в интервала (0, 2) и като F '(х) = 2 х> 0 и е' '(х) = 2> 0.
В този случай, уравнението на допирателната има формата: у-y0 = 2x0 · (х-x0). В точка x0 избере точка В1 (б; е (б)) = (2,2). Обръщаме допирателна към функция у = F (х) в точка В1. и означават точката на пресичане на допирателната и точка X1 оста Ox. Ние получи първата допирателна уравнение: у-2 = 2 · 2 (х-2), у = 4x-6. пресечната точка на допирателната и Ox оста: Х1 =
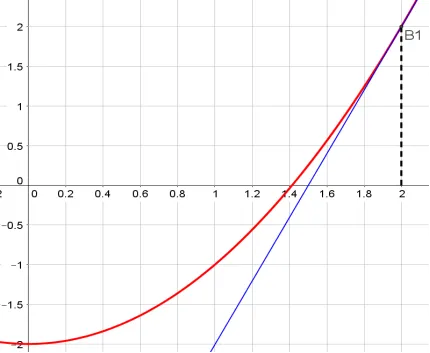
Фиг. 3. Изграждане на първата допирателна към графиката на функцията F (х)
След това ние откриваме, точката на пресичане на функция у = е (х) и перпендикулярна съставен на оста Ox чрез точка на X1. Ние получи точка В2 = (1,5; 0,25). Отново допирателна към функция у = F (X) в точка В2. и означават точката на пресичане на допирателната и Ox точка х2.
Уравнение втората допирателна: г-2,25 = 2 * 1,5 (х-1.5), у = 3x - 4.25. Точката на пресичане на тангентата и оста Ox: Х2 =.
След това ние откриваме, точката на пресичане на функция у = е (х) и перпендикулярна съставен на оста Ox през точка х2. Взимаме точка B3, и така нататък.
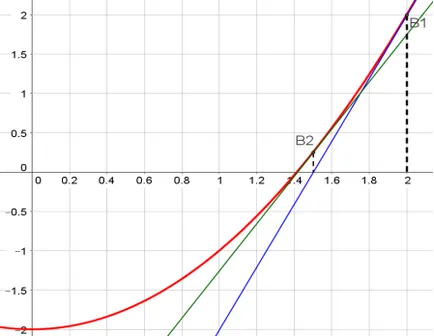
Фиг. 4. Конструиране на втората допирателна към графиката на функцията F (х)
Първият сближаване на корена се изчислява по формулата:
Вторият сближаване на корена се изчислява по формулата:
=
Третият сближаване на корена се изчислява по формулата:
По този начин, -тата корен приближение се изчислява по формулата:
Изчисленията се извършват, докато, докато един мач на знака след десетичната запетая, които са необходими в отговора, или определената точност е - да неравенството | XI-XI-1 |