метод Matrix за представяне на алгоритъм, публикувано в списание "млад учен"
Библиографска описание:
В работата счита алгоритъм за матрица-предикат форма в модулен и матрично-предикат форма. Показано е, че при висока оскъдица на получената матрица може да се заменя с таблицата, която е, да се създаде алгоритъм в таблица-предикат форма.
Думи: алгоритъм, предикат, матрица, маса, графика.
Класическата Идеята на алгоритъма - вербална или под формата на блок-схеми - макар и да е леко възприемане и яснота е от съществено значение за определен клас проблеми недостатък - ниска формализация. Това е особено важно в случаите на съставяне на алгоритми за паралелна обработка на информацията, и експлоатация на сложни многокомпонентни системи на няколко критерия. В тези случаи е необходимо да се намали нивото на евристични методи и да се повиши нивото на формализъм. Следователно, желателно е да се въведе алгоритъм в подредена структура. Такава форма на матрица и са, в структура, която включва елементи от теорията предикатното, задачите и метод, който се обсъжда по-долу.
Алгоритъмът Графично е представена последователност от взаимосвързани функционални блокове, всеки от които съответства на прилагане на едно или повече действия. Това изображение се нарича блокова диаграма или поточна диаграма, графика или диаграма на (GAW).
В момента алгоритми се третират като последователно структура, т.е. изпълнението на операциите, извършвани последователно.
Да разгледаме GSA (фиг. 1).
- върхове, които определят представянето на отделните операции ще се нарича функционални блокове или дялове на действие;
- върховете определяне логика (ред) на алгоритъма ще се нарича или предикативни логически блокове.
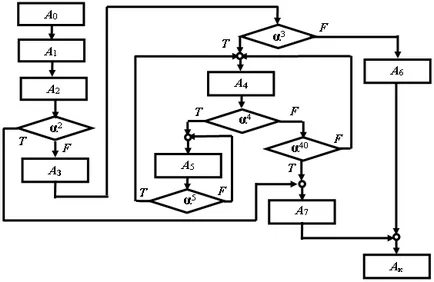
Фиг. 1. Графиката графика
Определяне на алгоритъма под формата на GAW има няколко недостатъка:
преход изпълнява една операция за извършване на друга в някои случаи не е определено, например, върховете А0 - A1 - A2, тук се разбира, че след операцията трябва да скочи А1 към стъпка А2, макар че такава преход не фиксирана;
условия, определящи реда на изпълнение на алгоритъма, често няколко логически функции са определени, например 4-α α 40, което усложнява алгоритъм анализ.
Първият от тези недостатъци се елиминира чрез комбиниране на два или повече оператори в едно действие, например, на върха А0 - A1 - А2 е заместен при 012 или в края на всеки от действията на функционалните оператори фиксирани края на техния обхват.
Вторият от тези недостатъци се елиминира чрез комбиниране на множество логически функции на един известни техники на булевата.
В резултат на тези операции, които ще бъдат наричани по-нататъшни операции на изпълнения, на проследяване алгоритъм да пристигне под формата на модулни единици (фиг. 2).
Прекъснатата линия маркирани модули алгоритъм, и Фигура (фиг. 3) показва изображението на алгоритъм в модулна конструкция, която е графика, Berge
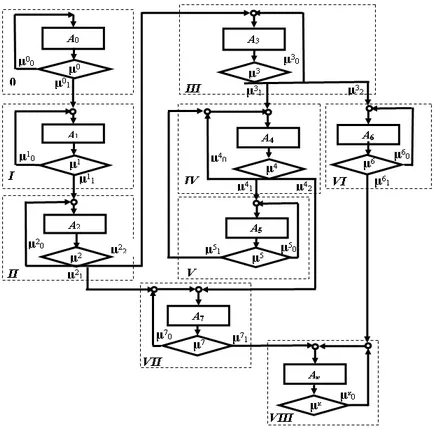
Фиг. 2. "Doopredelonnaya" графика диаграма

Фиг. 3. алгоритъм на изображението в модулен дизайн
Алгоритъмът може да бъде настроена във формата на графика (фиг. 4), на върха на която се разделя на два несвързани комплекти, което означава, че броят ще бъде двойна.
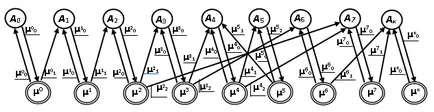
Фиг. 4. Определяне на алгоритъма под формата на двойна графиката
Използвайки метод матрица-предикат графика представяне [1-3] и представяне на алгоритъм модули (фиг. 3), алгоритъмът позволява да се създаде в матрица (фиг. 5).

Фиг. 5. Модулна представяне на алгоритъма под формата на матрица-предикат
Това представяне на алгоритъма ще призове modulnymvmatrichno-предикат форма.
Квадратна матрица М алгоритъм А, дава под формата на матрица-предикат има неизменност свойства, описани обект със същите номера, когато едновременно заместване на редове и колони на съответната двойка с друг номер [4].
Равен такава операция с матрицата М А, различни функционални и предикативни алгоритъм върховете в противоположни посоки. Като резултат, ние получаваме описанието на същия алгоритъм като М А * в различна форма (фиг. 6).
Това представяне на алгоритъма ще бъдат посочени под формата на матрица-предикат.
алгоритми за работа под формата на матрица-предикат дава почти всяка операция върху тях. Недостатъкът е, че когато голям брой компоненти с резултатите на екрана или хартията дава много обемисти. Това се дължи на високото разреждането на оригиналната матрица. Например, квадратна матрица (фиг. 5) включва елемент 324, и най-значимите (не е нула) 47.

Фиг. 6. Функционално алгоритъм predikativnoepredstavlenie в матрична форма предикат
Такава връзка, и нула важни елементи на матрицата предлага използва за представяне маса алгоритъм е както следва.
Да приемем, че разглеждания алгоритъм (като оператор, а логиката оператор) представляват истинските стойности dvenadtsatimestnogo предикат, описващи въпросния процес.
второ, трето и четвърто място Процесът на определен компонент funktsionirovniya. Определени с 4-ти до 12-ти се определят свойствата, времето на позиция funktsionirovniya и други характеристики на обекта в даден момент от процеса.
Първата и последната линии определи връзката между истински стойности на предиката. Тази форма на присвояване алгоритъм ще се нарича маса предикат.
Таблица-предикат форма задача на алгоритъма е представена по-долу.
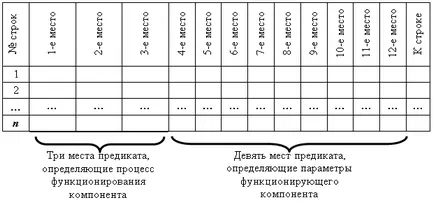
Фиг. 7. Подробности на референтната алгоритъм в таблица форма предикат
Да разгледаме матрица-предикат представяне алгоритъм в модулен начин (Фиг. 5) и прехода към маса форма предикат а. Фигура (фиг. 8) са представени в табличен вид предикат-обсъдени алгоритъм задача.
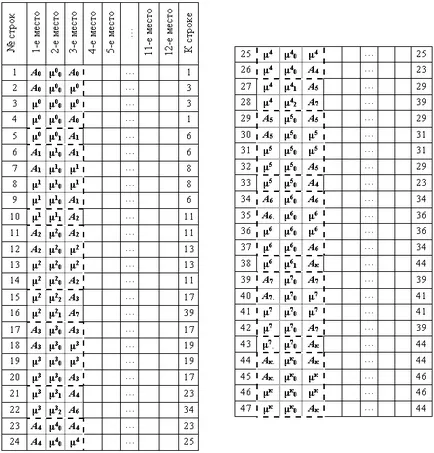
Фиг. 8. предиката Таблицата форма предварително определен алгоритъм в модулна форма
По този начин, освен конвенционалните методи алгоритъм може да бъде разположен в матрица-предикат или предикат-таблична форма.
Основни понятия (генерирани автоматично). алгоритъм, матрица-предикат форма, алгоритъмът Задача на алгоритъма, изпълнението на алгоритъма, задачата на алгоритъма, класическа представяне на алгоритъма, въпросът за представяне на алгоритъма, идеята на модули алгоритъм модулни представяне на алгоритъма, алгоритъм за изпълнение, предикатив връх алгоритъм, поточна диаграма, графика-схема алгоритъм на графика графиката на модулите на алгоритъм, задачи форма на алгоритъм, алгоритъмът квадратна матрица, задача алгоритъм фрагмент, предиката е представена от матрична д алгоритъм.