Mathcad се изгради една кутия и произволен многоъгълник в 3d

MathCAD: изграждане на кутия и произволни полигони в 3D

В действителност, триизмерен куб в MathCAD могат да бъдат представлявани от "тайна функция" Polyhedron ( "# 11") (за повече информация в тази моя статия). Но какво, ако не се наложи само на куб и кутия или, например, Х. Й. Z ос не искат да харчат, когато те държи MathCAD - в ъгъла на 3D-област, и своето място в основата?

Standard означава, някак си не се случи, но ако забавно пътуване с matkadovskim вектор контекст, след което можете да правите почти всичко. Такива като казва VF Точки. Извеждане. там също са забавни, и полезно.

В тази бележка вече имаме кода, за да се изгради на мястото или сегмент в триизмерни графики. Ако е така, от сегментите може да се състои от всеки кадър, в това число и в кутията. За простота, ние ще направим своя страна успоредно на осите, а паралелепипеда задават два диагонално противоположни върха на P и Q.

За да MathCAD видим прекарал ос през началото, ние определяме за допълнителна функция Ox. Oy. Оз (на графиката - синята линия). Размерът на осите зависи от стойността на. показващи границите на региона, за да бъдат показани са едни и същи и в трите измерения. Това е цялата изчисление:

Кутия и дясна оси в Mathcad

Както може да се види, не е необходим метод функция канализиран точка, това е достатъчно за предаване на координатите на два колонни вектори на всеки елемент 3, показва координатите на противоположни върха на паралелепипед.

Що се отнася до прекъснатата линия, тя може да бъде прекъсната линия сегменти, и е възможно и лесно да се изгради произволен многоъгълник върхове от N, написани на вектора на 3 ред (размер на N елементи) х последователност, Y и Z-координати на върховете и след това напиши във вектора колона. И двата метода показват например, и в двата случая, начупена линия zamknom на вземане на координати на последната точка съвпада с първите координати.

Mathcad: изграждането на наклонен в триизмерното пространство

Вторият вариант определено е за предпочитане, тъй като не изисква дублиране на данни, призовава за допълнителна функция Point. и, в допълнение, е изграждането на един обект, вместо N различни обекти. Следователно, всички разбити лесно пребоядисване или да го замени дебелина.

В заключение, ние конструираме редовно тетраедър с връх А в основата и на връх Б в (1,0,0). На този етап С, и лежи в равнина XY координати ще бъде (1/2 корен (3) / 2, 0). и "горен" връх S - координати (1/2 корен (3) / 6, в основата (6) / 3).

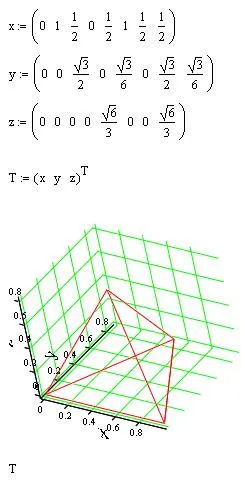
Mathcad: как да се изгради редовен тетраедър с дадените координати на върховете

Координати на първата точка не съвпада с координатите на последната, но нашата фигура е затворен. Само един от ръбовете се пресича два пъти, а именно, че сме на ръба на "маршрут" AB - BC - Калифорния - AS - SB - BC - CS. Около всички краища на тетраедър, които имат само един път, не е възможно за всеки ръб.