Магически квадрати от домино

Фиг. 7 показва квадратен от 18 кости на домино, забележителен факт, че сумата от точки на всеки от неговите серии - надлъжна, напречна и диагонал - и един

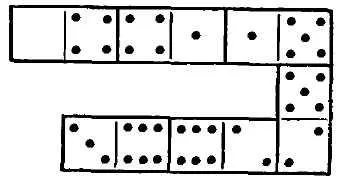
Същите 13. Тези площади отдавна са наречени "магически".

Вие сте поканени да направят няколко от същия 18-каменни магически квадрати, но с различен брой точки в един ред. 13 - най-ниската сума в редиците на магически квадрат, съставени от 18 кости. Най-голямата сума - 23.

Прогресия на домино.

Можете да видите на фиг. 8 шест кости домино, посочени в съответствие с правилата на играта и се характеризира с това, че броят на точките на костите (в двете половини на всяка кост) се увеличава с 1. серия започва с 4 и се състои от следния брой точки:

Тази поредица от числа, които увеличават (или намаление) на една и съща стойност се нарича "аритметична прогресия". В нашата поредица, всеки брой е по-голям от предишния, по един; но прогресия може да бъде всеки друг "разлика."

Предизвикателството е да направи няколко 6-каменни прогресии.

ИГРА НА 15 или взети

Пословичен кутия с 15 номерирани квадратни пулове има любопитна история, която няколко играчи знаят. Ние разкажа за думите си немският изследовател игри, математика W. Аренс.

Фиг. 9. Играта на 15.

"Около половината преди един век - в края на 70-те години - се появи в САЩ," играта на 15 ", тя се разпространи бързо и благодарение на безбройните броя на играчите, тя пленени, се превърна в реална социална катастрофа.

"Същото се наблюдава от тази страна на океана, в Европа. Тя може дори Конка да видите в ръцете на пътниците кутии с 15 шашки. Собствениците на офиси и магазини се отчаяли от ентусиазма на своите служители и трябваше да ги забрани да играят в часовете на обучение и търговия . Хазяи развлекателни съоръжения умело използват тази мания и организираха големи хазартни турнири.

Играта е проникнала дори в най-тържествените зали на германския Райхстаг. "Все още мога да видя сивокоси хора в Райхстага, имайки се концентрира в ръцете си квадратна кутия" - припомня известния географ и математик Zigmund Gyunter, бивш заместник по време на епидемия хазарта.

"През 1880 г., хазарт е достигнал висока температура, както изглежда, най-високата си точка, но скоро след това на тиранина е бил победен, и победен математици оръжия математическата теория на игрите е установено, че много от задачите, които могат да бъдат предложени, решими само половината; .. Другият не е разтворим не трикове.

"Стана ясно, защо някои задачи не отговарят на най-упорито и защо организаторите на турнира се осмелили да назначи огромна премия за разрешаване на проблеми. Във връзка с това надмина всички игри изобретател, който предлага на издателя на вестника в Ню Йорк в продължение на

Неделя добавка зле с премия от $ 1000 за своята резолюция; като издателят се поколеба, изобретателят изрази пълната готовност да направи име сума от собствения си джоб. Името на изобретателя Самюъл (Сам) Лойд. Той стана широко известен като композитор на остроумни задачи и разнообразие от пъзели. Интересно е, че в Америка се получи патент за игра, измислена от него не успя. Според указанията, той трябваше да представи "работен модел" за изпълнението на партида; той предложил на служителя задачата на патентното ведомство, а когато последният попита, дали той е решим, изобретателят трябваше да отговори: ". Не, това е математически невъзможно" "В този случай - последвано от възражение - не може да бъде работещ модел, а не модел и не патент." Лойд бе доволен от това решение - но най-вероятно би било по-устойчиви, ако е предвидено безпрецедентен успех на изобретението си "[Този епизод, използвана от Марк Твен в романа." American претендент ".]

Ето собствената си история на изобретателя на играта на някои от фактите своята история:

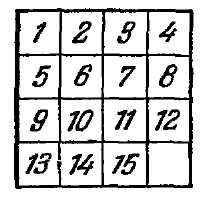
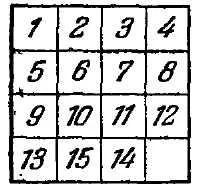
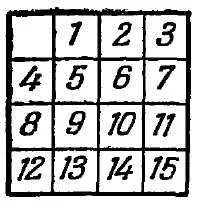
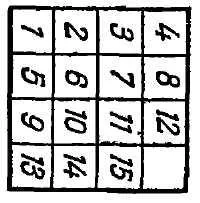
"Жителите дългогодишен царството на остроумие, - казва Лойд, - Спомням си как в началото на 70-те години, направих целия свят, за да мисля кутия с преместването на пуловете, е станала известна като" Игра 15-те "(Фигура 10) Петнадесет проекти бяха.. подредени в квадратен кутия в правилния ред, и само пуловете 14 и 15 са пренаредени, както е показано в придружаващия илюстрацията (фиг. 11). целта е да се последователно преместване на пуловете, да бъдат приведени в нормалното си положение, при което, обаче, редът блоковете 14 и 15 трябва да бъдат коригирани.

"Наградата от $ 1000 предлага за първи правилното решение на този проблем, никой не е заслужена, въпреки че неуморно решен този проблем. Те разказаха смешни истории за търговци, забрави, защото от това им се отворят магазини, на вековни длъжностни лица, през цялата нощ не се използва . под улична лампа, търсене на начин за решаване на никой не му попречи да се откаже от търсенето на решение, защото всички се чувствах уверен в своите успехи чакат навигатори, да речем, се дължи на играта бяха поставени върху техните кораби, заседнал, машинисти се извършва от гарите. фермери Те хвърляха плугове ".

Ние ще представят на читателя наченки на теорията на играта. В пълна си вид тя е много сложна и е тясно свързан с един от отделите на алгебра ( "теория на детерминанти"). Ние се ограничим с някои от съображенията, изложени Б. Аренс.

"Задачата на играта е обикновено до чрез последователни движения, разрешени от присъствието на свободно поле за трансфера на всяка първоначална място 15 придържа към нормалното, т.е. такава, в която бомби са в реда на номерата им: .. горния ляв ъгъл едно, нали .. - 2, след това 3, след това в горния десен ъгъл 4, в следния ред от ляво на дясно: 5, 6, 7, 8, и т.н. Това е нормално крайния местоположение представяме тук на фигура 10 ..

"Представете си сега на мястото, в което се намира на 15 блока в колоритния бъркотия. Близо движение винаги могат да бъдат доведени до проверка на едно място, което заема на фигурата.

. "Възможно е също така, без да докосвате дама 1 олово бомба 2 от съседна място в дясно след това, без да докосвате на блоковете 1 и 2, могат да бъдат поставени Дама 3 и 4 naih нормално място, ако се случи да се намери в последните две вертикални редове, а след това лесно да доведе в този регион и след това следващия движение за постигане на желания резултат. Сега най-горния ред 1, 2, 3, 4 се предоставя в ред, и по-нататъшно манипулиране на пуловете опираме това число няма. по същия начин се опита сложим в ред и втори Онлайн: 5, 6, 7, 8, е лесно да се види, че тя винаги постига . Gibly Освен това, през последните два реда от пространството трябва да бъде доведена до нормално положение пулове 9 и 13, също така е винаги възможно От всички изброени по реда на блоковете 1, 2, 3, 4,5,6,7,8,9 и 13 по-долу. аудио не се премества ;. остава малък участък от шестте области, където един е свободен и останалите пет са заети пулове 10, 11, 12, 14, 15 на случаен принцип в тази шест места част винаги могат да бъдат приведени в нормалното пространство пулове 10, 11 12. Когато се стигна, последния ред на пулове 14 и 15 ще се намира в нормално ред Или в обратна посока (фиг. 11). В известен смисъл, че читателите могат лесно да проверят по въпроса, имаме следния резултат.

"Всяко начална позиция може да бъде доведен до местоположението или Фиг. 10 (позиция I), или фиг. 11 (позиция II).

"Ако местоположение, които за краткост означена с буквата С. може да се трансформира в положение I, след това, очевидно, обратното е възможно - да се преведат на позиция I на позиция С. След като всички движения на пулове са обратими: ако, например, в схема I, може да се бомбардира 12 пуснати на свободно поле, то е възможно да се премести тази веднага да премине отново през обратното движение.

"Така че, ние имаме две такова споразумение серия, че разпоредбите на една серия могат да бъдат превърнати в нормален I, а другата серия -. За позиция II и обратно, от нормалното местоположението, можете да получите всяка една позиция на първата серия, както и от място II - всяка една позиция на втория серия. Накрая, всеки две места, принадлежащи към една и съща серия, могат да се трансформират един в друг.

? "Възможно ли е да отиде по-далеч и се съчетаят двете места - аз и II могат да бъдат строго доказано (ние няма да навлизам в подробности), че разпоредбите на те не се превръщат в един от друг във всеки брой ходове защо всичко на големия брой парчета от разположения е разделена на две коренно различни серии :. 1) тези, които могат да бъдат превърнати в нормален I: е - позиция разтворим, 2) тези, които могат да бъдат превърнати в позиция II и следователно в никакъв случай да бъдат прехвърлени към нормалната местоположението: It - разпоредби за позволявайки който naznachalis е огромни бонуси.

"Откъде знаеш дали посоченото място принадлежи на първа или втора серия? Един пример ще изясни това.

"Ние считаме, че такова споразумение.

. "Първият ред на блокове в ред, като на втория, с изключение на последните шашки (9) Този блок се осъществява, което в нормалния мястото принадлежи 8.Shashka 9 следва да raneeshashki 8: е нормалният ред на присвояване по-нататък" бъркотия "О. проверка 9, да кажем: тук е заболяване място един това допълнителни пулове намерят "очакване" за пулове 14, е поставен на три места (блокове 12, 13, 11) преди нормалното си положение; тук ние имаме 3 разстройство (14, преди 12. , 14-рано 13 ;. 14, преди 11) Всички сме Брой 1 + 3 = 4 разстройство нататък, Br. Ashka 12 били поставени пулове 11, и по подобен начин, блокът 13 преди шашки 11. Това дава още 2 разстройство. Общо имат 6 смущения. По същия начин, за всяко местоположение определя общия брой на смущения, предварително освобождаване на последно място в долния десен ъгъл. Ако общият брой смущения като в горния случай, дори, на предварително определено място могат да бъдат доведени до нормална край, с други думи, той принадлежи към разтворим. Ако броят на инверсии е нечетен, местоположението принадлежи към втората серия, т. Е. (приема да бъде четен брой нула безредици) до неразтворим.

"С по-голяма яснота, въведена тази игра по математика, бивш трескава страст в това хоби в момента е немислимо. Математика е създал цялостна теория на играта, теорията не оставя никакви съмнителни точки. Резултатът от мача не зависи от всеки шанс, а не от изобретателен, както в други игри, но от чисто математически фактори, определящи го с абсолютна сигурност. "

Нека сега се обърнем към пъзелите в тази област.

Ето няколко решими проблеми, изобретени от изобретателя на играта:

Първата задача Лойд.

Въз основа на разположението, показано на фиг. 11, доведе пулове в правилния ред, но със свободно поле в горния ляв ъгъл (фиг. 13).

Втората задача Лойд.

Въз основа на местоположението на фиг. 11 Завъртете кутия четвърт оборот и се движат пуловете, стига те да не вземат оформление фиг. 14.

Третата задача Лойд.

Преместването на пуловете в съответствие с правилата на играта от позицията на Фиг. 11, завъртете квадратчето в секцията "магически квадрат", а именно, нестабилна място, така че сборът от цифрите е във всички посоки е 30.

Улавянето пъзели, свързани с играта на домино и 15, ще остана в рамките на аритметика. Обръщайки се към пъзела на крокет съда, стигаме отчасти в геометрията.

Предлагам следните пет задачи крокет играчите.