Линейна функция и нейната графика, висша математика - прости и лесни

В последния урок разгледахме пряка пропорционалност и нейната графика. Сега ще разгледаме по-сложна функция, а като комплекс само малко по-сложно.

Да разгледаме примери на функции

Пример 1. Разстоянието между двата града (означен А и В) е 30 км. Мотоциклиста ляво на точка В, в посока, обратна на А, със скорост от 50 km / h. За часа на ездача ще премине км и ще бъде град А на разстояние от км. Ако означим разстоянието от буквата А за ездач на града, зависимостта на дистанцията на времето може да бъде изразена чрез формулата

,

Пример 2 ученик купил бележника 5 рубли за брой и дръжката 10 рубли. Ние означаваме броя на преносими компютри, закупени с буквата, а цената на всички покупки. Тогава ние се

,

където х - число.

дефиниция

В този пример, се срещнахме с функциите, които се определят от формулите

,

където - независима променлива, а и - броя.

Тези функции се наричат ​​линейни функции.

Линейна функция е функция, която може да бъде определена чрез формулата на формата, където - независима променлива, и и - някои номера.

Директен пропорционалност, което сме учили в последния урок, също се отнася до линейна функция, но това е специален случай, когато второто число не присъства или е равна на нула.

Сега нека да разберете какво графика е линейна функция.

Като пример, да вземе проста функция, с обща формула, и го сравни със стойност директно пропорционална на същите стойности.

Вече като се започне от стойностите на двете функции може да се види, че за всяка стойност на стойността на аргумента х функция от 4 единици по-малки от функцията стойност

Сега ние се изгради графики

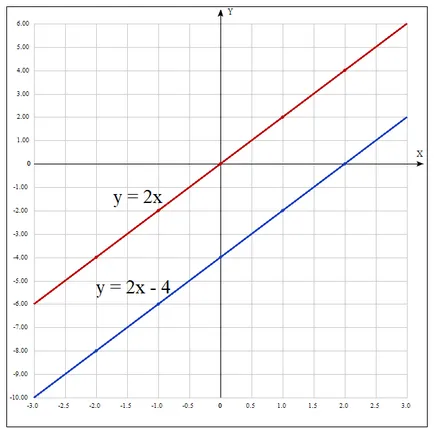
Както можете да видите на графиката, линиите за данни са успоредни.

Графика на функцията, където к ≠ 0, има една права линия, успоредна на линията.

Между другото, има случаи, в които к = 0, уравнението взема формата, в която графиката на функцията ще бъде успоредна на оста X, и имащи стойност, равна на броя аргумент б.

Например, ние изграждане на графика на функция у = 2

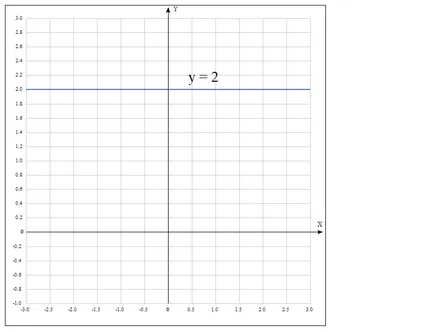
Тази функция е линейна.

За да се построи линията само две точки, тъй като пряко пропорционално на една точка е известен, ние открихме само една точка, в една и съща линейна функция, ние трябва да намерим 2 точки.

Е, това е всичко, както ти казах всичко, така че можете да приключите.