Лаплас уравнение и хармоничен

Ще започнем с най-простите и най--елиптични уравнения, че именно Лаплас уравнение. Това уравнение уравнение има формата

Тук е (х) - дадена функция. Ако е (х) ≠ 0. след това уравнение зададена (1) е нехомогенен уравнение на Лаплас. Ако е (х) = 0 имаме хомогенна уравнение Лаплас

Нехомогенни уравнение на Лаплас често се нарича уравнението на Поасон.

В по-подробен запис на уравнението на Лаплас - нехомогенни-роден и униформа - са както следва:

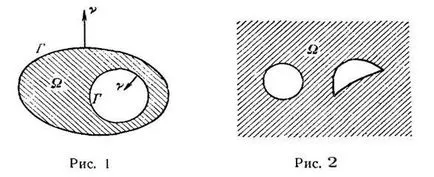
Помислете затворена повърхност F не е непременно свързан "и нека F ограничава обхвата на # 8486; крайната (. Фиг 1) или безкраен (фигура 2) в двата SLE-чайове предполага ", че самата повърхност D е ограничен. Budemizuchat поведение хомогенна Лаплас уравнение в тези области.

U (х) се нарича хармонична в краен регион # 8486;, ако тя е в тази област е два пъти непрекъснато диференцируема и отговаря на хомогенна уравнението на Лаплас.

Ние казваме, че ф (х) функцията хармонично в областта на безкрайно-крайните # 8486;, ако при всяка точка от тази област, разположена в края или началото на региона, ф (х) е два пъти непрекъснато диференцируема, udovletvoryayi хомогенна уравнение на Лаплас на безкрайност и е от порядъка

,така че за достатъчно голяма | х | неравенство

където m - измерение на пространството и C - е някакъв постоянен-ценен. В случай на двумерен област (т = 2) Състояние (3) означава, че chaet хармонична в безкраен домен е ограничена в безкрайността.

Ние се подчертае, че определянето на хармонична функция otno-sitsya само за случая на откритата площ (т.е. множеството отворен свързан ..); Ако говорим за хармонична на функции в затворена зона, от това имаме предвид, че функцията е хармонично в широк открито поле.

Ние също така имайте предвид, че определението за хармонична функция не налага никакви ограничения върху поведението на функцията на границата.

Пример 1: Ако # 8486; - безкраен регион, ф функция (х) = 1 хармонична само ако m = 2. Ако т> 2. в безкраен региона, тази функция нехармоничен. Въпреки това, гуарова monichna във всяко крайно поле, за всеки тон.

Пример 2. В равнина функция двуизмерен

където Z = х + IV. хармонично във всяка област, която не съдържа произхода.

Пример 3. Функция

Z = х + Iy. хармонична в кръг | Z |

Пример 4: функция на две променливи ф = х 2 + Y 2 не е Xia хармонично във всеки домейн, защото не отговаря ryaet-хомогенна Лаплас уравнение

Пример 5 Функцията ф = Х2-y2 хармонично във всеки краен солна област.

В двумерен равнина на трансформация конформна не променя хомогенна уравнението на Лаплас. В случай на всеки, така че не е така, но все още е налице трансформация че Perevi-ди всяка хармонична функция в една и съща хармонична. Тази трансформация Келвин, който се точката

х (XI, Х2. х) за х "(h'i x'2. x'm). симетрични по отношение на точка X на сферата с радиус R центриран в основата, и солна дадена функция и (х) на функцията

Спомнете си, че точките х и х "се нарича симетрична по отношение на по-горе споменатите райони, ако те лежат на една и съща лъч излъчвана от произхода, а ако | х | • | х '| = R2. Декартова координатна съгласува симетрични точки са свързани с

Обикновено, макар и доста тромава изчисление води до връзката