Лаборатория на ъ-ъ - проблема, страница 1

Печалбата от продажбата на единица продукция от първия тип е 2 ден. ф втори вид - 3 ден. U ..

Задачата е да се изгради капацитета на производство на програмата, която осигурява най-добрата възвръщаемост на неговото прилагане.

С печалбата от продажбата на данни на всеки тип продукт, ние можем да се превърне Таблица 1 Таблица 2.

Норма разходи на ресурси на стоки

Общо ресурси

Печалба от продажба

EMM образуват задачата.

Нека x1 и x2 - количество на 1-ви и 2-ри форми, необходими за получаване на максимална печалба. Тогава EMM ще изглежда така:

X = (х1, х2) - вектор, където F (X) → макс и ограничения удовлетворен

Ние решаваме полученото линейно програмиране проблем графичен метод.

Ние изграждане на задачата за ОРС. Условия nonnegativeness полуравнина определено с granichnyim права x1 = 0 и х2 = 0, съответно.

Линейно уравнение описва множеството от точки, лежащи на една права линия. Линейно неравенство описва определена област на самолета. Определя коя част от равнина, описана от неравенството

Вграден прав. Тя преминава през точките (0, 6) и (6 0). С цел да се определи кой отговаря на самолета, трябва да изберете всяка точка не принадлежи на една права линия. Ние избираме точката на произход (0, 0) и заместване на неравенството получи 0≤12. Това твърдение е вярно, следователно неравенството съответства на долната половина на самолета.

По същия начин, ние определяме равнината на други ограничения.

Пресечната точка на тези по-ниски половин равнини, всеки от които се определя от съответния неравенството на системата и отговаря OAVSD на условия без неотрицателност определя многоъгълник. Координатите на всяка точка, която принадлежи към домейна са валидни решение на проблема. (Фигура 1)

За намирането на максималната стойност на обективната функция, когато нанася решаване на проблема на линейното програмиране използване на градиент вектор, координатите на които са частични производни на обективната функция.

Този вектор показва посоката на стръмните промяна в обективната функция. Директен 2x1 + 3x2 = А (- константа) е перпендикулярна на вектора на градиент. Преместването на линията на ниво в посока на вектора толкова дълго, тъй като оставя извън тунела за вторично разреждане. Резервен поле момент по време на това движение и е с максимален момент, в нашия проблем е точка С (Фигура 1). За да намерите координатите на тази точка е достатъчна за решаване на две уравнения на линиите, получени от съответните ограничения и даване в точката на пресичане на максимум.

Стойността на целевата функция в този момент е:

макс е (X) = 2 * 3 * 4 + 2 = 14

Заключение: Печалбата на компанията ще бъде оптимизиран и ще бъде 14 парични единици ако продуктът от първата вид ще бъдат издадени в размер на 4 продукти, както и продукти от втората вида, в количество от 2 продукти.

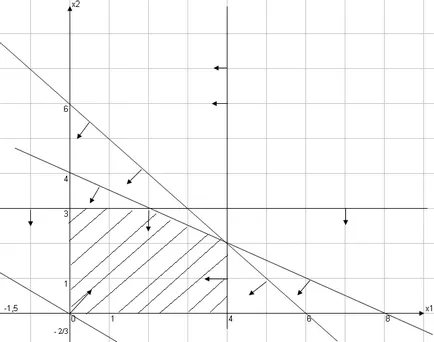
Фигура 1. Графичен разтвор ZLP.

Ние формулира и решаване на двоен проблем. Използване на двойственост теорема, ние решаване на проблема в получаването на приходи от продажбата на ресурси не е по-малка от сумата, получена в процеса на производство.

Ние построи двойна проблема за оригинала:

Използването на първата двойственост теорема, ние имаме:

F (X *) = Z (Y *), т.е. оптималните стойности на обективни функции са еднакви.

Тъй като оптималната план на първоначалния проблем Х1 = 4; х2 = 2, и състоянието на не-негативизъм, след това от теоремата на комплементарна отпуснатост за двойния брой Y1 и Y2 * уравнение притежава:

Z (Y *) = 12 * 8 + 0,5 * 1 + 0 * 16 + 0 * 12 = 14

Dual оценка намери правилно.

Икономически смисъл задачи.

Печалбата на компанията ще бъде оптимизиран и ще бъде 14 парични единици ако продуктът от първата вид ще бъдат издадени в размер на 4 продукти, както и продукти от втората вида, в количество от 2 продукти. Състав и решаване на проблема до минимум, ние виждаме, че при оптимални програмни производство и векторни ресурси, производствените загуби са нулеви оценки.

За производството на четири вида продукти, използвайки три разтваря суровина. Запаси от суровини, Правилника за неговото дебит и продажна цена на единица на всеки продукт са показани в таблица лице: