Комплекс за движение на точка пример за решаване на проблема

Един пример за решаване на проблема с комплекс за движение на точка. Point се движи в права линия по протежение на плоча. Плаката се върти около фиксирана ос. Определена абсолютната скорост и абсолютен ускорение на точка.

Теорията се използва за решаване на следния проблем е представен на страницата "комплекс за движение на точка, Кориолис теорема".

състояние проблем

Рисуване за състоянието на проблема

Правоъгълната плаката се върти около фиксирана ос от закона 6 φ = Т2 - Т 3 3. положителната посока на референтната ъгъла ф е показано на стрелката на фигури дъга. Оста на въртене OO 1 се намира в равнината на плочата (плоча се върти в пространството).

Чрез движи плоча по права линия BD точка М. дадено право на относителната му движение, т.е. зависимост S = AM = 40 .. (T - т 2 3) - 40 (а - в сантиметри, т - в секунди). Разстояние В = 20 см. Фигурата показва точка М на позиция, в която е = AM> 0 (за S <0 точка M находится по другую сторону от точки A ).

Виж абсолютната скорост и абсолютната ускорение на точка М в момент Т1 = 1.

Инструкции. Тази задача - да се комплекс за движение на точка. За да го реши, че трябва да използвате теоремата за добавяне на скорости и ускорения на оставка (Кориолис теорема). Преди извършване на всички изчисления трябва да бъде при условията на проблема за определяне където точка М на пластината по време Т1 = 1. и да представлява една точка в тази позиция (и в нито е показано на фигурата на проблема).

решение на проблема

. Предвид: б = 20 6 см ф = т 2 - 3 т 3. S = | AM | 40 = (т - т 2 3) - 40. 1 т = 1 гр.

Определяне на положението на точката

Определяне на позицията на точката от време, т = 1 т = 1 гр.
40 S = (Т 1 - т 2 1 3) - 40 = 40 (1 - 2 · 1 3) - 40 = -80 см.
тъй като е <0. то точка M ближе к точке B, чем к D.
| AM | = | -80 | = 80 cm.
Направете чертеж.

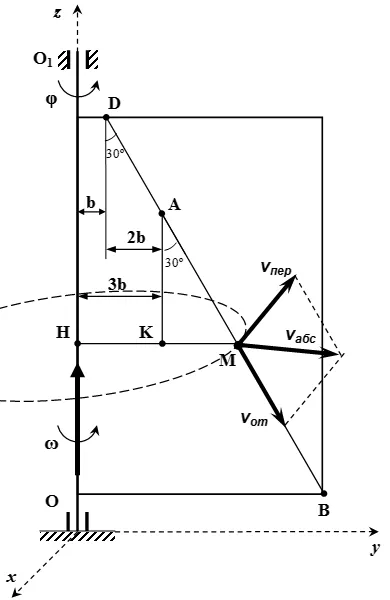
Относителна, преносими и абсолютната скорост на точка M

Определяне на абсолютната скорост на точка

Според теоремата за събиране на скорости. абсолютната скорост на точка е вектор сумата от относителните скорости и портативни:
.

Определяне на относителната скорост на точката

Ние се определи относителната скорост. За да направите това, ние считаме, че плочата е фиксирана и на точка M прави предварително определен движение. Това е точката М се движи по права линия BD. Разнообразяване и по време на т. Ние считаме, компонентата на скоростта по посока СД:
.
В момент Т = 1 т = 1,
см / сек.
Тъй като. векторът е насочена в посока, обратна на BD. Това означава, че от точка М до точка Б. относителна модул скорост
V от = 200 см / сек.
Представлявано от вектор на фигурата.

Определяне на транслацията скоростта на точката

Определяне скоростта на движение. За тази цел, ние приемаме, че точка М е неподвижно свързан към плоча и плочата извършва предварително определено движение. Това означава, че плочата се върти около оста OO1. Разнообразяване φ по време на т. Ние считаме, ъглова скорост на въртене на плочата на:
.
В момент Т = 1 т = 1,
.
Тъй като. вектор ъглова скорост е насочено към положителен ъгъл на завъртане φ. това е, от точка O до точката, O1. Устройството за ъглова скорост:
ω = 3 и -1.
Изобразяват вектор ъгловата скорост на плочата на фигурата.

От гледна точка М пропуснат HM OO1 перпендикулярна на оста.
Когато преносима точка за движение M се движи по окръжност с радиус | HM | центриран в точка Н.
| HM | = | HK | + | KM | 3 = б + | AM | грях 30 ° = 60 + 80 · 0.5 = 100 cm;
Portable скорост:
vper = ω | HM | = 3 х 100 = 300 см / сек.

Векторът е насочено по допирателната към окръжността в посоката на въртене.

Определяне на абсолютната скорост на точка

Ние определи абсолютната скорост. Абсолютната скорост на точка е вектор сумата от относителните скорости и портативни:
.
Ние предлагаме на фиксирана ос координатна система Oxyz. Z ос е насочена по оста на въртене на плочата. Да предположим, че в даден момент от време, х е перпендикулярна на оста на плоча, у ос лежи в равнината на плочата. Тогава векторът на относителната скорост се крие в YZ равнина. транслационни вектор скорост е насочен противоположно на оста х. Тъй като вектор, перпендикулярна на вектора. след това от Питагоровата теорема, абсолютната скорост на модула:
.

Определяне на абсолютната ускорението на точка

Според теоремата на прибавяне на ускорение (Кориолис теорема). абсолютен точка ускорение е равна на сумата от вектор относителните, преносими и Кориолис ускорения:
.
където
- Кориолис ускорение.

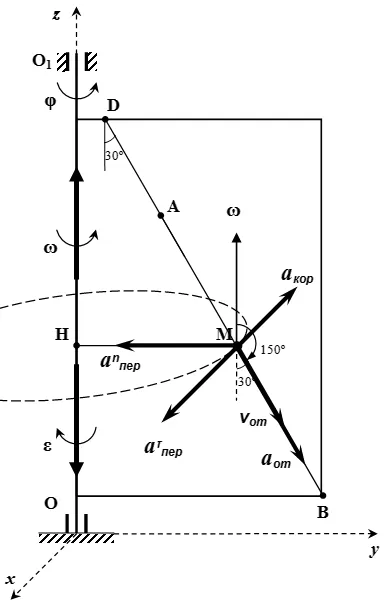
Относителни, преносими, Кориолис и абсолютната ускоряване на точката М

Определяне на относителната ускорение

Ние определи относителната ускорение. За да направите това, ние считаме, че плочата е фиксирана и на точка M прави предварително определен движение. Това е точката М се движи по права линия BD. Разнообразяване на два пъти е по време на т. Намираме компонента ускорение по посока СД:
.
В момент Т = 1 т = 1,
cm / и 2.
Тъй като. векторът е насочена в посока, обратна на BD. Това означава, че от точка М до точка Б. относителна модул ускорение
АОТ = 480 cm / и 2.
Представлявано от вектор на фигурата.

Определение преносим ускорение

Определяне на ускорението на преносим. Когато преносим точка движение М е неподвижно свързан към плочата, т.е. движи в кръг с радиус | HM | центриран в точка Н. разлагат преносим ускорение на допирателната към окръжността и нормалното ускорение:
.
Разнообразяване на два пъти φ по време на т. намери проекцията на ъгловото ускорение на плочата на ос OO 1:
.
В момент Т = 1 т = 1,
и -2.
Тъй като. вектор ъглово ускорение се насочва в посока, обратна на положителен ъгъл на завъртане Ф. това е, от гледна точка О1 О. модул ъглово ускорение на точка:
ε = 6 -2.
Изобразяват вектора на ъгловото ускорение на плочата на фигурата.

Преносим тангенциално ускорение:
а τ платно = ε | HM | = 6 · 100 = 600 см / сек 2.
Вектор насочени тангенциално към периферията. Тъй като вектор ъглово ускорение се насочва в посока, обратна на положителен ъгъл на завъртане Ф. Той е насочен в посока, обратна на посоката на въртене положителен φ. Това е насочено към оста х.

Преносим нормално ускорение:
а н платно = ω 2 | HM | 2 = 3 х 100 = 900 cm / и 2.
Вектор е насочен към центъра на кръга. Това означава, че в посока, обратна на у оста.

Определяне на Кориолис ускорение

Кориолис (въртене) ускорение:
.
вектор ъглова скорост е насочено по оста Z. Векторът относителната скорост е насочено по линията | DB |. Ъгълът между тези вектори, е равна на 150 °. Чрез имот вектор продукт,
.
вектор посока се определя от правило. Ако копчето за палеца на свой ред от позиция до позиция. винт палеца ще се движат в посока, противоположна на оста х.

Определяне на абсолютната ускорението

Absolute ускорение:
.
Ние проектираме този вектор върху ос уравнение ЮЯ координатна система.

абсолютен модул ускорение: