Количествени и качествени характеристики на информацията

Информационни мерки обикновено се разглеждат в три аспекта: структурни, Статис-и-статичен семантичен.

Структурната аспект, структурата на информационните масиви и измерването им на просто чрез преброяване на информационни елементи или комбинаторни методи. Структурната подход се използва за оценка на възможностите на информационните системи, независимо от тяхното прилагане.

В статистическата подход използва концепцията за ентропия като мярка за несигурност, който взема предвид вероятността от възникване и информационното съдържание на съобщението. Статистически подход взема предвид специфичните условия на използване на информационни системи.

Семантичната подход позволява да се подчертае, полезността или стойността на съобщението за информация.

Структурно информационна мярка

Информацията е представена по един под формата на съобщение. Основно звено Messaging - символ. Герои, събрани в групи - думата. Посланието, издаден под формата на отделни думи или знаци, винаги се предават на материала и формата на енергия (електрически механизъм, светлинно звукови сигнали).

А информация разграничение непрекъснато и дискретни (фиг. 2.4).

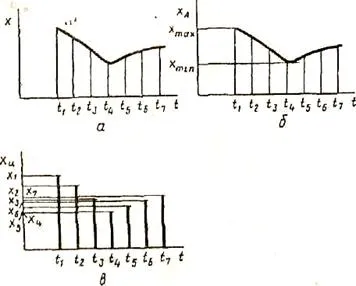
Фиг. 2.4. Начини за представяне на информация

функцията х (т), показана на Фиг. И 2.4. Тя може да бъде представена в непрекъснат (фиг. 2.4б) и дискретни (фиг. 2.4) видове. В непрекъснат формата на тази функция може да поема всички реални стойности в даден диапазон на изменение на аргумент Т, т.е. множество от стойности на непрекъсната функция за неопределено време. В отделна форма на функция х (т) може да получи веществото правителствена стойности само за определени стойности на аргумента. Независимо дискретност малък интервал (т.е. разстоянието между съседни стойности аргумент) или избира множество дискретни стойности на аргумента функция за предварително определен диапазон на промяна (ако не е безкраен) е ограничен (ограничена).

При използване на информация за структурата на мерките взети под внимание само на дискретна структура на съобщението, броят съдържа информационни елементи, връзките между тях. В структурен подход, различна геометрия, комбинаторна и добавки информационни мерки.

Геометрично измерване включва измерване на параметър на геометричния модел на информационните изолационна мнения (дължина, площ, обем) в дискретни единици. Например, геометричен Coy информация модел може да бъде линия на единица дължина (Фигура 2.5 и - една дума е 0 или 1), квадрат (фигура 2.5 б -. Двуцифрени дума) или куб (фигура 2.5 по - три цифри дума). Максималният възможен размер на информация на предварително определени структури определя модел информационен капацитет (система), която се определя като сума от дискретни стойности на всички измервания (координатите).

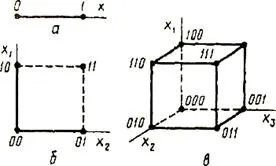
Фиг. 2.5.Geometricheskaya информационен модел

Комбинираното информацията се определя като броя на елементите, тъй като броят на комбинациите (знака). Възможното количество информация, равен на броя на възможните комбинации и пермутации на разположения на елементите. Комбинирането на символи с една дума, състояща се само от 0 и 1, промяна на значението на думите. Помислете за две двойки думи 100110 и 001101, 011101 и 111010. Те проведоха изключителна пермутация от цифри (промени мястото на знаков бит в броя на - категорията премества от ляво на дясно).

Добавка мярка (Hartley мярка), съгласно които размерът на данни се измерва в двоични единици (бита), най-често. Концепциите за дълбочина и продължителност.

Дълбочината на броя (р) - броя на символите (елементи) взети да представлява инфор-мацията. Във всеки един момент само един се реализира характер. номер Дълбочина съответства на системата на база брой.

номер дължина (п) - броя на позициите, необходими и достатъчни, за да представляват номера дадена стойност. Дължина съответства на броя на битовете на системата за брой.

За дадена дълбочина и продължителност на броя на номера, които могат да бъдат представени, ще
N = р п. стойност N е неудобно за капацитет на информация оценка. Хартли влезе добавка двоичен логаритмична мярка, която позволява да се изчисли количеството на информацията в двоични единици - бита:

Това е единица за информация за Хартли.

Ето защо, една-битова информация съответства на един елементарен събитие, което може или не може да се случи. Тази мярка на количеството информация е полезна с това, че дава възможност да се работи като мярка за броя. Количеството информация, при което броят на двоични символи еквивалентни на 0 или 1. Ако има няколко източници на информация общо количество информация

където (Qk) - размерът на информация от източник к. Най-логаритмична мярка на информация дава възможност да се измери количеството на информацията, и се използва в практиката.

Статистическа информация мярка

Статистическата информация се въвежда мярка за количеството на информацията, теория, според която не се счита за самото събитие, но информацията за това. Този въпрос е разработен
Шанън в "Избрани произведения на теорията на информацията." Ако съобщението
а често срещаната събитие, вероятността за което е близо до единство, това е съобщение за получател малко информация. Просто по-малко информация, докладвана soby-tiyah, вероятността за което е близо до нула.

Събитията могат да се разглеждат като възможен изход от определен опит, както и всички резултати от този опит, формират пълна група от събития. Шанън представи концепцията на несигурност на ситуацията, възникващи в хода на експеримента, наричайки го ентропията.

Entropiyapolnoy група събитие е количествена мярка на своята несигурност и следователно-TION, съдържание на информация, количествено изразени като средна вероятност функцията на набор-ността на всеки от възможните резултати от експеримент на. Размерът на информация, получена в резултат на експеримента, една и съща несигурността отпада по време на този опит.

Вероятностен подход се обясни най-добре чрез пример с участието на хвърляне солна правилни зара с N аспекти (най-често е случаят на костна хекс: N = 6). Резултатът от този експеримент може да бъде загуба на лицето с един от следните знаци: 1, 2. Н.

Разглеждане на цифров количеството, което измерва несигурността - ентропия (означена с Н). Стойности на Н и N са свързани функционална връзка:

и функция F се увеличава, и неотрицателно определен (в разглеждания пример) за N = 1, 2. 6.

Процедурата за хвърляне на зарове:

- готов да хвърли костите. Опитът изход е неизвестен, т.е. Има известна несигурност, ние означаваме H 1;

- кост хвърлен. Информация относно резултатите от този експеримент се получава, това количество данни е означен с I;

- означаване на несигурност на експеримента след неговото изпълнение през Н2.

За размера на информацията, получена по време на опит упражнение, да вземе несигурността разлика "преди" и "след" експеримент:

Очевидно е, че в случая, когато се получава специфичен резултат, който бе отстранен несигурността (H 2 0). Брой на получената информация съвпада с оригиналния ентропията. С други думи, несигурността, която се съдържа в опита, в съответствие с информацията относно резултатите от този опит. Значение Н 2 може да бъде различна от нула, например, в случаите, когато по време на експеримента има следния аспект със стойност по-голяма от три.

Следващото нещо е да се определи вида на функцията F. Ако варира броят на лицата N и броя на хвърля зарове (тази стойност се означава с М). Общият брой на резултатите (M вектори с дължина 1, състояща се от символи, 2. N) е равна на N в степента на М:

По този начин, в случай на две хвърля зарове с шест страни, имаме: X = 6 2 = 36. В действителност, всеки X е резултат от определена двойка (X 1, X 2), където X 1 и X 2 - съответно първи и втори крайните резултати отливките (общо такива двойки - X).

Ситуацията с актьорския състав на M пъти костта може да се разглежда като сложна система, състояща се от отделни независими подсистеми - ". Единични хвърляния костите" Ентропията на една такава система е M пъти по-дълго от ентропията на системата (така наречената "принципът на адитивност на ентропията"):

където * - умножение знак.

От формулите, получени мярка Hartley:

Важна с въвеждането на количество е въпросът за това какво да се вземе за мерна единица. Н е равно на една когато N = 2. С други думи, като информационни единици получи информация брой свързани с извършване на експеримент, състояща се от получаване на една от двете еднакво вероятни резултати (пример на такъв експеримент може да служи като хвърляне на монетата където са възможни два изхода: "Eagle "" опашки ").

В случая, когато вероятностите за различни резултати не изпитват еднакво (но имат вероятност Pi), мярка на ентропията се изчислява с помощта на формулата Shannon:

Като пример, може да определи количеството на информацията, свързана с появата на всеки знак в съобщения, написани на руски език. Ние приемаме, че българската азбука се състои от 33 букви и на знак "пространство" за отделни думи. Според формула получаваме: п> 5 бита.