Как да се изгради фрактал набор от Apollo

Част 2 от 2: Изграждане на Аполон Редактиране

Много от Apollo е под формата на красив фрактал дизайн от спад в размер на обиколки. Математически много Аполон безкрайно сложна, но ако сте с помощта на компютърна програма, или традиционни инструменти за рисуване, в крайна сметка ще достигне точката, в която би било невъзможно да се направи по-малък кръг. Имайте предвид, че колкото по-точно да чертаете кръг, толкова повече те ще се срещнат различни Аполон.

Започнете с един голям кръг. Първата ви задача - просто направи едно голямо, идеално гладка кръг. По-голямата кръга, толкова по-трудно може да бъде вашата фрактал, така че се опитват да се построи окръжност, която позволява на размера на хартията, или така че да може напълно виждате на екрана в графична програма.

Начертайте кръг по-малък в първия кръг, който ще я докосне в един момент. Така че, начертайте кръг в кръга на първата ни, то ще бъде по-малко от главницата, но все пак достатъчно голям. Точният размер на втория кръг е до вас, тъй като няма фиксирана сума. Все пак, нека да се направи втори кръг, така че да не заема половината от главния кръг. С други думи, чийто център - това е средната радиуса на по-голям кръг.

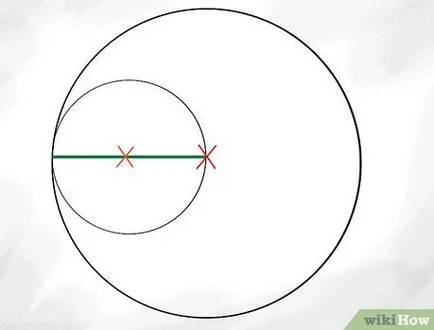
• Имайте предвид, че определени Аполон всички кръгове са допирателни към друг. Ако използвате в изграждането компас кръгове пресъздаде този ефект чрез поставяне на острия край на компас в средата на радиуса на основната окръжност и регулиране на компас молив, така че тя просто докосва ръба на кръга, а след това се направи по-малък вътрешен кръг.

Равен кръг до идентичен на вътрешната периферия. Така че нека да се направи още един кръг до първата. Кръгът трябва да бъде допирателна на двете окръжности: най-външния и по-ниско вътрешната, което означава, че и двете вътрешни обиколка граничат точно в центъра на голям.

Прилагането на теорията на Декарт, за да се изчисли размерът на тези кръгове. За миг, спрете рисуване. Сега, когато имаме трите среди в фрактал, можем да използваме Декарт теорема да се намери радиуса на следващия кръг, който ще изготви. Забележка Декарт теорема уравнение г = A + B + C ± 2 (√ (а х б + б х в + с х а)). където а, Ь и с е кривината на три кръга допирателна и г - кривината на кръга, допирателна към всичките три. Следователно, за да се намери радиуса на следващата ни кръг, нека да се изчисли кривината на всеки един от съществуващите ни кръг, докато не може да намери извивката на следващия кръг, а след това се изчисли радиус му.

• Да се ​​определи радиуса на външния периметър като 1. Защото другите кръгове са вътре в нея, ние се занимаваме с "вътрешен" извит (вместо външни), и поради това ние знаем, че тя е отрицателна. - 1 / г = -1 / 1 = -1. Тъй като кривината на голям кръг е равна на 1.
• Радиусът на малък кръг е половината от радиуса на големи, т.е. 1/2. Тъй като те обиколка в контакт един с друг и главния кръг Външно, ние трябва да се справят с външния кривината положителен. 1 / (1/2) = 2. Следователно, кривината на малък кръг е равно на 2.
• Сега знаем, че а = -1, б = 2 и с = 2 в теорема ни уравнение на Декарт. Да се ​​изчисли г:
  • г = A + B + C ± 2 (√ (а х б + б х в + с х а))
  • г = -1 + 2 + 2 ± 2 (√ (-1 х 2 + 2 х 2 + 2 х 1))
  • г = -1 + 2 + 2 ± 2 (√ (-2 + -2 + 4))
  • г = -1 + 2 + 2 ± 0
  • г = -1 + 2 + 2
  • г = 3. кривината на следващото периферно 3. От 3 = 1 / R, радиусът на този кръг е равна на 1/3.

Начертайте следващите няколко кръга. За да се направят следните две среди, като се използва радиуса, че току-що сте намери. Не забравяйте, че тези кръгове са допирателни към тези, чиято кривина е била използвана при изчисляване на картезианската теорема. С други думи, те ще се докоснат и първични и вторични кръгове. За тези кръгове докосват останалите трима, ще трябва да ги въвлече в откритото пространство над и под в основния кръг.

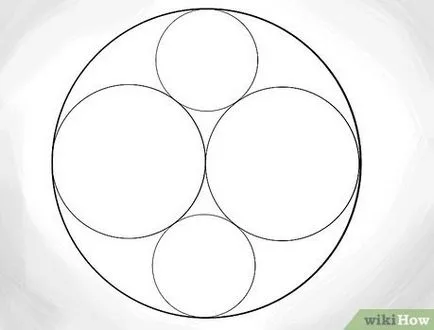
• Имайте предвид, че радиусът на тези кръгове е равна на 1/3. Измерва 1/3 от външния ръб на обиколката, а след това се направи нова. Тя трябва да е допирателна към всички три кръга наблизо.

По този начин поддържа добавянето обиколка. Тъй като те са фрактали, много Аполон безкрайно сложна. Това означава, че можете да добавите кръга по-малък и по-малък до основата на фрактал. Вие сте ограничени само от точността на вашите инструменти (или, ако използвате компютъра си, способността да се увеличи графична програма). Всеки кръг, колкото и малка да е, трябва да е допирателна към останалите три. За да начертаете кръг всяка следваща употреба на кривината на три кръга, допирателна към него за теоремата на Декарт. След това използвайте отговор точно се направи нов кръг.

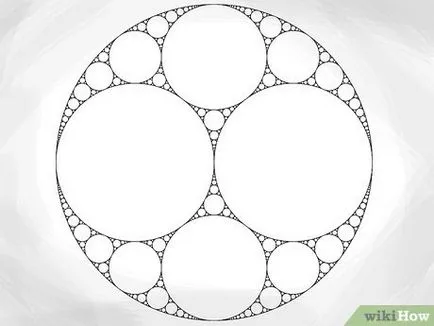
• Имайте предвид, че на снимачната площадка, които сме избрали да се изгради, симетрични, така че радиуса на окръжност, е същото като радиуса на окръжност, идентичен с него. Въпреки това, не всички набори Аполон симетрични.
• Нека разгледаме един пример. Да предположим, че след изграждането на последните няколко кръга, ние искаме да се направи кръг допирателната към нашата трета двойка и основния кръг. Кривината на тези кръгове е съответно 3, 2 и 1. Сега ние включваме тези номера в декартови теорема, се установява, че а = 1, б = 2 и С = 3:
  • г = A + B + C ± 2 (√ (а х б + б х в + с х а))
  • г = -1 + 2 + 3 ± 2 (√ (-1 х 2 + 2 х 3 + 3 х 1))
  • г = -1 + 2 + 3 ± 2 (√ (-2 + -3 + 6))
  • г = -1 + 2 + 3 ± 2 (√ (1))
  • г = 2, 6. Имаме два отговора! Въпреки това, ние знаем, че нашата нова кръг ще бъде по-малък от допирателната към него, така че ще има смисъл само да ценим кривината 6 (в радиус от 1/6).
  • Друг отговор, 2, всъщност се отнася до хипотетична кръг на "другата страна" на допирната точка на втория и третия кръг. Този кръг е допирателна към тези две среди, както и за главницата, но тя ще пресече тези от кръга, която току-що изготвен, така че може да се игнорира този отговор.

Като тест, опитайте се да се изгради асиметричен набор Аполон, промяна на размера на втория кръг. Всички комплекти Аполон започват да се изгради с една и съща - с голяма външна периферия, която е граница фрактал. Въпреки това, не е необходимо да бъде равна на радиуса на втория кръг на първата половина. Ние просто са решили да вземат тези номера за простота и лекота на разбиране. За забавление, опитайте се да се изгради нов набор от втория кръг на различен размер - това ще доведе до нови направления в научните изследвания.

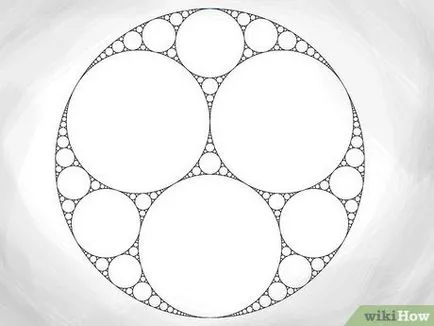
• Веднъж построен втори кръг (независимо от размерите му), следващото си действие трябва да бъде да се изгради една (или повече) от кръга, която се допира до втория и до основните външни периферии - не само правилен метод за това как да се изгради. След това можете да използвате теоремата на Декарт за определяне на радиуса на следните кръгове, както е показано по-горе.