Използвайки модерна програма Grapher на поуките от алгебра в гимназията, социална мрежа

ИЗПОЛЗВАНЕ НА УРОЦИТЕ PROGRAMMYAdvancedGrapherNA на алгебра в гимназията

МР - училище № 3 (област Mozhaisk, Москва).

В статията е обяснено в подробности как да използвате AdvancedGraphermozhno програма за изчертаване на алгебрични и тригонометрични функции в Декартова координатна система, за опознаването на функциите и да намерят деривата, примитивен, се изчислява площта на затворени фигури. Са примери за общи задачи в алгебрата класна стая в гимназията и предимствата на програмата на по-функционални изследвания.

Ключови думи: AdvancedGrapher програмни схеми, функции по разследването.

Учител, който е на компютъра има уникалната възможност да направят учебния процес по-визуална и динамичен с графичен програма AdvancedGrapher, която има огромен брой възможности, в това число, нека изградете таблици в полярна координатна система, както и линията, определена по параметри, опростяване на студентски труд строителните графици.

Да разгледаме характеристиките на използването на програма AdvancedGrapherna урок по алгебра в гимназията на.

1. Fix способността за изчертаване на графики в различни координатни системи.

2. Fix знанието на училище алгоритмичен език.

3. Fix математическите знания на тема: "Изследване функцията".

4. За да се развиват внимателност, логическото мислене.

Вид на урока. интегриран.

1. усвояването на студенти понятия за алгоритмичен език, математически език, познаване на тема изследване на функцията;
2. формиране на способности и умения на учениците, които работят с програма AdvancedGrapher;
3. развие способността да се чете информация и да я използват;

1. разработване на информационен интерес на учениците;
2. развитието на логическото мислене на учениците, паметта, вниманието;
3. формирането на информационна култура на учениците;

1. образование усърдие;
2. насаждане на учениците уменията на самостоятелна работа.

а) да се припомнят ключови думи на езиковото училище алгоритмичен:

- абсолютна стойност: ABS;

- запис тригонометрични функции: грях (х), COS (X) и др.

II. Работа в класната стая:

Използване на графиката се дефинира нанасяне функция:

1. Област на определяне.

2. монотонността на функция (т.е. увеличаване или намаляване интервали

3. Интервалите на постоянен знак:

4. четност или Од, т.е. е (Х) = F (х) - симетрично относителна

координатна ос; е (Х) = - е (х) - симетрично за произхода.

5. (точка графика на пресичане) нули:

6. екстремум точки: Maxy = []; miny = [].

Всеки учител и ученик знае как монотонни и трудоемки класове на функциите на научните изследвания, като понякога е трудно да се обясни на някои от етапите на изследването: специално квартала, в който има интонацията; асимптота на графиката, и др. Тази програма улеснява обяснението на материала и дава възможност на студентите да се научат трудните пасажи от материала по-бързо, тъй като тя дава възможност да се увеличи размера на графика, изпълнява допълнителни конструкции по-подробно и производство на цялостно изследване на функцията.

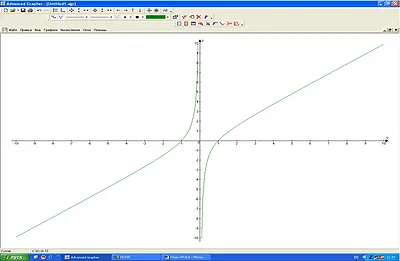
1) Добавяне на графика диаграма → → Информацията у (х) → (правят формула (х ^ 2 - 1) / х)) (Фигура 1) .. Получената графиката е показано на фиг. 2.

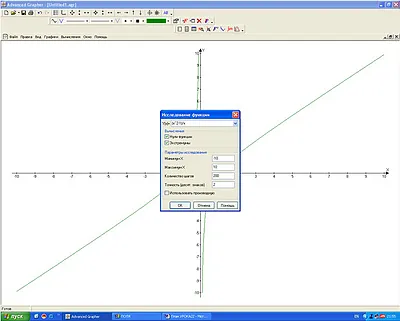
2) Изчисления Ц → изследвания функции (правят функция изцяло) → нули на екстремумите на функцията + + + мин макс (+ използване производно) (фиг. 3).

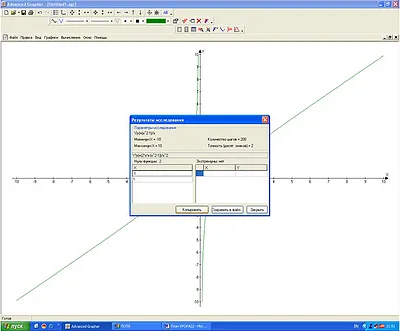
3) В резултат на изследването (производно)

б) крайности (фиг. 4).

4) В резултат на изследването без производното:

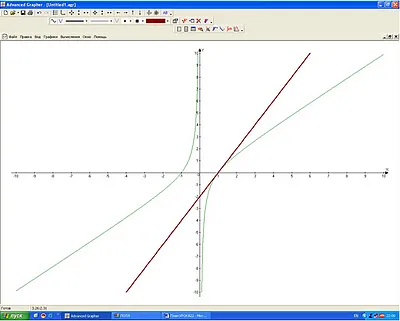
Tangent → Добавяне на график → Опции → OK (формула).

Резултатът е показан на Фиг решения. 5.

График всяка функция може да бъде изградена от точки, т.е. в таблицата.

Таблица → Формула стойности (х ^ 2 - 1) / х от -10 до 10 на стъпки от 1 → → Изчисленията функция формула (х ^ 2 - 1) / х → лечение.

Ние разгледани подробно разтвора на пробата №1, също са изследвани и графиките на примери на функции №2 - №4.

(Графики → → имуществени комплекси, определени от тригонометрични

№4. Построяване на графики на функции (не само една)

Използването на графични програми могат да изградят и в полярна координатна система, а също и линията, определена по параметри. В допълнение, той привлича графици и направления, които са определени от уравнения или неравенства, за изпълнението на които уроците отнеме много време. Да разгледаме rezultatat конструира като графика.

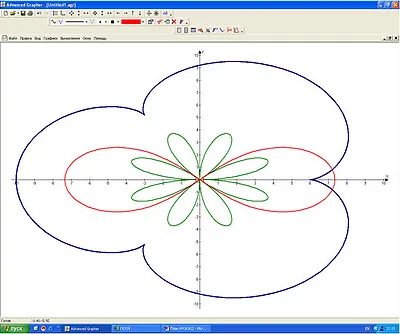
№5. В полярни координати за парцел следните функции

(Изграждане на последователно извършване на една и съща графика):

3) (2 х + у 2) 2-54 (х 2 - Y 2) = 0 - в Декартова координатна система [2] (виж фигура 6).

№6. За самостоятелно изпълнение. Построява се графика на функцията:

III. Обобщавайки резултатите от урока.

IV. Домашна работа: Напишете изграждане работа графики алгоритъм номер 6.