Инерционният момент на равнинни сечения
Аксиален разрез инерционен момент (втори момент на област или втория инерционен момент) около оста х е сумата от продукти на елементарните области Da от квадрата на техните разстояния от оста, която е числено равно на интеграл
$$ J_x = \ int_y ^ 2DA $$
И по отношение на у ос:
$$ J_y = \ int_x ^ 2DA $$
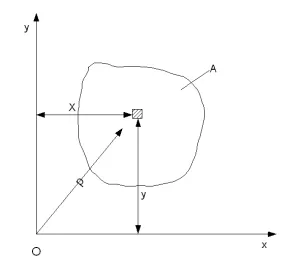
където у - разстояние от DA елементарен площ на х (виж фигурата) на вала,
х - разстояние от DA елементарен площ на оста у.
Polar инерционен момент по отношение на дадена точка
(Наречени стълбове) е сумата на продукти от елементарни области Da по квадрата на разстоянието им до този момент:
$$ J_ = \ int_ ^ 2DA $$
където [математика] \ р [/ математика] - Da далеч от мястото на пръта за който се изчислява полярен инерционен момент.
Центробежни инерционен момент на осите х и у е сумата от произведенията на елементарните области DA на разстоянието от тези оси:
$$ J_ = \ int_x у Da $$
където X, Y - разстояние от DA елементарен площ на осите х и у (виж фигурата).
Центробежната инерцията може да бъде положително, отрицателно, а в специалния случай на нула. Когато взаимно перпендикулярни оси х и у или един от тях са оси на симетрия на фигурата, относителните оси на центробежни инерция е нула. [Math] J_ = 0 [/ математика].
Polar инерционен момент на някои - всяка точка е равна на сумата от аксиални инерционни моменти около две взаимно перпендикулярни оси, минаващи през тази точка. $$ J_ = J_x + J_y $$
Връзката между моментите на инерция около оси, успоредни
Формули за инерционни моменти оси паралелно предаване:
$$ J_> = \ int_ (Y + а) ^ 2DA = J_ + 2aS_x + а ^ 2А $$
$$ J_> = \ int_ (х + б) ^ 2DA = J_ + 2bS_y + б ^ 2А $$
$$ J_y_1> = \ int_ (Y + а) (х + б) DA = J_ + aS_y + bS_x + ABA $$
Инерционният момент за всяка ос, равно на инерционния момент
по отношение на централната ос, успоредна на тази, както и продукта на квадратни фигури на квадрат разстоянието между осите.
Инерционният момент спрямо оста на симетрия се нарича централната точка на инерцията.
От формулите, от това следва, че от момента на инерция около централната ос по-малко от инерционния момент за всяка ос noncentral раздел паралелно към центъра.
Връзката между моментите на инерцията при включване оси
$$ J_ = J_x защото ^ 2 \ алфа + J_y грях ^ 2 \ алфа - J_ грях (2 \ алфа) $$
$$ J_ = J_x грях ^ 2 \ алфа + J_y защото ^ 2 \ алфа + J_ грях (2 \ алфа) $$
и центробежно инерционен момент: $$ J_ = * грях (2 \ алфа) + J_ COS (2 \ алфа) $$
Някои свойства сглобяеми инерционни моменти
- Размерът - дължина 4 (обикновено 4 cm)
- Аксиални и полярни инерционни моменти - стойности са винаги положителни защото произволно координати на мястото са включени във формулата в квадрата.
- При завиване оси количество аксиални инерционни моменти не се променя. $$ J_ + J_ = J_x + J_y $$
- Полярен инерционен момент за аксиално точка е сумата от моменти на инерция около две взаимно перпендикулярни оси, минаващи през тази точка: [математика] J_p = J_x + J_y [/ математика]
- Инерционният момент на съставния секцията е сумата от моментите на инерцията на елементите на секцията.