Howtodoit - на дискриминантата на квадратното уравнение (получаване)

Често, изучаването на основите на математиката, ние приемаме за даденост много или дори всички, дори не мисля за това, тъй като тя е получена или как да стигне до определена формула. Как тогава, страхувам се, че аз не разбирам от къде идва толкова проста и дискриминантен на квадратно уравнение от вида:

Писането е израз на лист хартия, исках да го реши, без да знаят всички добре познати формули на учебната програма. Започнах с това, което привлече графиката на уравнението. Резултатът е един вид парабола:

В горната част на параболата да намерите много прост. Производната на този етап трябва да бъде равна на нула. Производното на квадратното уравнение:

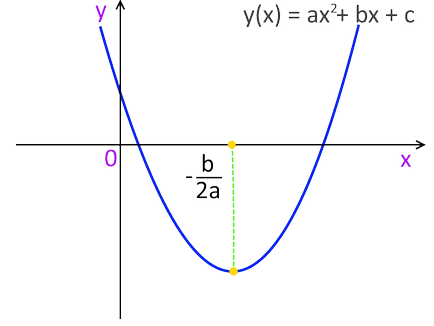
Е., Ние получена за върха на параболата. От друга страна ние искаме да се намери (и) стойности, при които стойността на функцията ще бъдат равни. В графиката ясно видими тези точки на пресичане:

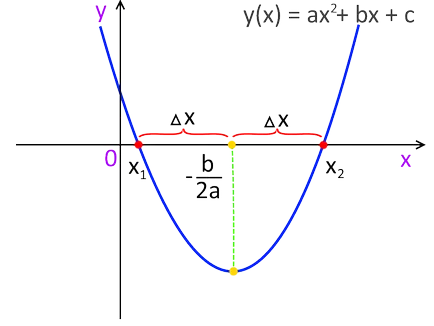
От графиката на параболата - симетрични, разстоянието от зададената точка на пресичане координати. След това корените на квадратното уравнение ще бъдат:

Ние замени трябвало решение за първоначална уравнение:

След опростяване получаваме:

Резултатът е познато на всички рекорда:

Това е всичко! С помощта на прости математически операции (с изключение на производни) води до получаване на желания резултат. Това рекорд:

и призова дискриминантен. Какво друго да кажа за дискриминантата? Влизане е подчертана в учебната програма само за удобство и няма вълшебна не е така. По-интуитивно е израз:

който има геометрична смисъла - е дължината на интервала, определен във втората снимката. За геометричния смисъл дискриминантен съди за себе си!