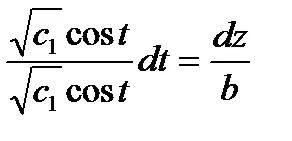градиент свойства - studopediya
1 0 Градиентът е насочено по нормалата към нивото на повърхност (или към линия ниво, когато поле е плосък).
2 0 Градиентът е насочен в посока на увеличаване поле функция.
3 0 модул градиент е най-деривати области napravleniyuvdannoy точка:
Тези свойства го инвариантна характеристика градиент правят. Те казват, че gradU вектор показва посоката и големината на най-големите промени в областта на скаларна в даден момент.
Забележка 2.1. Ако функция ф (х, у) е функция на две променливи, векторът
Той се намира в равнината на кислородния.
Нека U = U (X, Y, Z) и V = V (X, Y, Z) диференцируема в (X, Y, Z) функция M0 точката. След това имаме следните равенства:
а) град () =; б) град (UV) = VgradU + UgradV;
а) град (U V) = gradU gradV; ж) ж) град =. V;
г) gradU (= gradU, където. U = U () има производно.
Пример 2.1. Предвид функция U = х 2 + Y + Z 2 2. Определяне на градиента на функцията на точка М (-2, 3, 4).
Решение. Според уравнение (2.2)
,
.
Ниво повърхности на полето за скаларно са семейство сфери х 2 + Y + Z 2 2. вектор gradU = (- 4, 6, 8) е нормален вектор равнини.
Пример 2.2. Виж градиента на скаларно поле U = х-2y + 3Z.
Решение. Според уравнение (2.2)
Ниво повърхности на полето за скаларно са равнина
х-2y + 3Z = С; вектор gradU = (1, -2 и 3) има нормален вектор на семейството на самолети.
Пример 2.3. Виж максималната повърхност наклон лифт U = х у в точка М (2; 2; 4).
Пример 2.4. Намери единичен вектор нормално ниво на повърхността на скаларна областта U = х 2 + Y + Z 2 2.
Решение. равна повърхност на вътрешната сфера Fields х 2 + Y + Z 2 2 = C (C> 0).
Градиентът е нормално към повърхността на ниво, така че
. Определя вектор нормално към повърхността на слой в точка М (х, у, Z). За получаване на единичен вектор нормална експресия
.
Пример 2.5. Виж градиента на U =. където постоянните вектори, г е радиус вектора на точка.
След това:
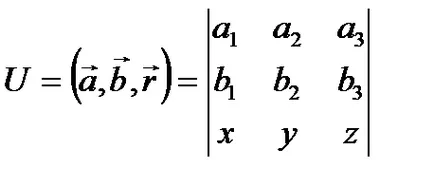
Пример 2.6. Намери наклона на разстоянието. където Р (х, у, Z) - проучени точка поле, P0 (x0, Y0, z0) - фиксирана точка.
Решение. Ние имаме - посока единица вектор.
Пример 2.7. Виж ъгълът между наклона на функцията в точката M0 (1,1).
Решение. Ние считаме, градиенти на тези функции в точката M0 (1.1), ние имаме
; Ъгълът между gradU и gradV точка M0 се определя от уравнението
Пример 2.8. Намерете производната по посока на вектора на радиус е
Решение. Ние считаме, наклона на тази функция:
Заместването (2.5) в (2.4) дава
Пример 2.9. Виж точката M0 (1, 1, 1) посока на най-голяма промяна на скаларно поле U = XY + YZ + XZ и величина от най-големите промени в този момент.
Решение. Най-големите промени в посоката, указана от вектора поле Градиент на U (М). Ние го намерите:
И след това. Този вектор определя посоката на голямото увеличение на полето в точката на M0 (1; 1: 1). Големината на най-голямата промяна на терена в този момент е равно на
.
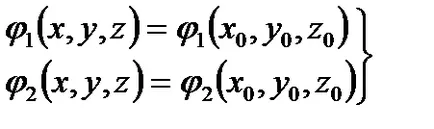
Пример 3.1. Намерете най-векторни линии на поле вектор, който е постоянна вектор.
Решение. Има толкова
Диференциални уравнения векторни линии
Увеличаването на числителя и знаменателя на фракцията за първи х и втората у-нататък, в последния пакет и се добавя termwise Z. Използването на пропорциите на имота, получаваме
. следователно xdx + ydy + zdz = 0, което означава,
х 2 + Y + Z 2 2 = А1. А1 -const> 0. Ние сега се размножават числителя и знаменателя на първата фракция (3.3) на С1. второ -на c2. трета c3 и добавяне, срок от термин, ние получаваме
. където С1 DX + С2 ди + c3 DZ = 0
Необходими уравнения на векторни линии

Тези уравнения показват, че векторни линии са резултат от пресичането на области с общ център в основата, с равнина, перпендикулярна на вектора. Това означава, че векторни линии са кръгове, чиито центрове са на права линия, преминаваща през началото с посоката на вектора. Кръгове равнина перпендикулярна на права линия.
Пример 3.2. Намери вектор поле линия, преминаваща през точката (1,0,0).
Решение. Диференциални уравнения векторни линии
следователно имаме