Гибс ефект
Принципът на последователното приближение на първоначалната форма ясно видими в долната графика модел. Той също така може да се види, както и причините за колебанията в реконструкцията на скокове на функциите, които се наричат на Гибс ефект. Ако промените броя на мандатите на серията обобщи Гибс ефект няма да изчезне. Не променя спрямо колебанията амплитуда (по отношение на амплитудата на шок) и относителната затихване (при скорост на постепенно намаляване на колебанията на амплитудата по отношение на максималното освобождаване) само се променя честотата на пулсация, честотата на който се определя от последните сумират хармоници.
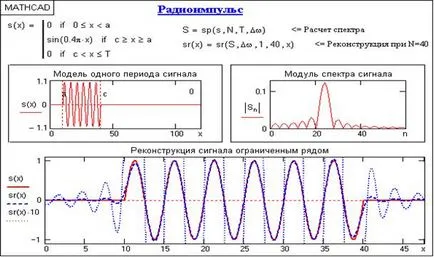
Гибс ефект винаги се случва, когато много сериозни нарушения на монотонни функции. На състезание ефект е максимален, във всички останали случаи, амплитудата на пулсация зависи от характера на нарушението монотонна. Един пример за това явление Gibbs за радио импулс е показано на фиг. 4.6 (използва програма на фиг. 4.4 показва реконструирания сигнал точки с увеличаване на мащаба на 10).
Фиг. 4.7 показва пример на серия разширяване на един период на Т Фурие = (а, в) моделиране на периодичен сигнал кв (х), представено с информационен сигнал и (х) в сумата с шумов сигнал. Шум спектър подобен на спектъра на бял шум (шум на равномерно разпределение върху спектъра на честоти на енергия).
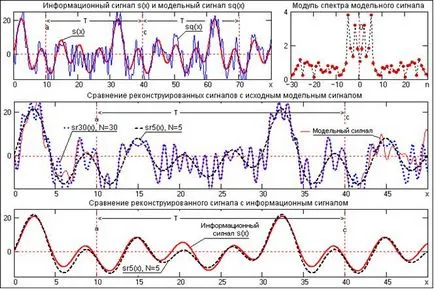
В моделиране сигнал информация спектър честота на сигнала гама справедливо разпределяне ясно. Възстановяване сигнал ограничен брой хармоници Фурие само информационен сигнал (сигнал SR5 (х), N = 5) дава загладени форма на вълната на минималната средна квадратична несъответствие с модел сигнал за даден брой отношение на поредицата, но само през периода на разширение (а, в) и най-точният сближаване с информационния сигнал. С увеличаване на броя на реконструкция в серия Фурие реконструиран сигнал започва да се доближава до модел сигнал, но само на периода на Т = (А, С), при което несъответствието с увеличаването на информационния сигнал. Имайте предвид, че спектърът на сигнала може да се определи и няколко периода на сигнала, което увеличава точността на реконструкцията на информационния сигнал.
Серията на Фурие може да се разложи и произволна периодична функция дефинирана (ограничена нарязани от друг сигнал и т.н.) в интервала (а, б), ако ние не се интересуваме от поведението му извън интервала. Въпреки това, трябва да се помни, че използването на (4,1-4,6) автоматично означава периодичен разширение на тази функция извън предварително определен интервал (в двете страни на него) с периода Т = б-а. Така на феномена на Гибс може да възникне слот ръбове ако сигналът скача в краищата на нивото на сигнала не го съвпадат и формира в периодичен повторение, както е показано на фиг. 4.8. Когато разширяването на оригиналната функция в ограничен брой Фурие и неговата преработка в честотната област е действително преработена в не едно и също време основната й функция и реконструиран от ограничен брой на Фурие.
Пресичането на Фурие серия от функции, определено изкривяване винаги съществува. Но при ниска гранична част от сигнал енергия съотношението на (с бързи функциите на затихване спектри), този ефект може да бъде трудно да се различи. В състезанията и прекъсване се проявява най-ясно.
Page генерирана за: 0.006 сек.