Геометрия Gia по математика

Задача 8 от геометрията на ДПА в математика

Най-простият задача да геометрията на ДПА в областта на математиката. Въпреки това, за да се реши, че е необходимо да има ясна представа за основните понятия на училище курс на геометрия, свързани най-вече с темите на "Квадрат", "подобни триъгълници", "отношенията между двете страни и ъгли на триъгълник" и "Обиколка и площ на кръг." В същото време като преподавател по математика, мога да кажа, че самият познаване на теорията на тези въпроси е крайно недостатъчно, за да се срещне успешно с предизвикателствата. решаване на геометрични проблеми умения, генерирани в течение на времето по един систематичен и последователен обучение под ръководството на учител.

Пример 1. страна на правоъгълен трапец формиране на база с голям ъгъл от 30 °, е равно на 4. Виж областта на трапеца, ако тя е равна на основата 2 и 5.

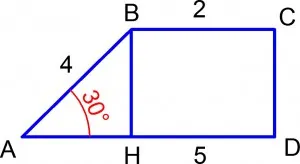
BH - височината на правоъгълен трапец ABCD

Основите на трапеца е от страните и техните половин сумата (половината сума), равна на височината на правоъгълен триъгълник се търсят, за които по дефиниция правоъгълен триъгълник синуса на малък ъгъл, ние имаме: това е,

Така областта на трапеца е равна на произведението на половин сумата на базите на височина от 2, т.е. 7.

Задачата за независимо решение №1. Страната на трапец формиране на база с голям ъгъл от 30 °, е равна на 3. Откриване областта на трапеца, ако основата са, съответно, 2 и 6.

Задача 14 от геометрията на ДПА в математика

Вписан ъгъл - ъгълът на върха на който се намира на кръг, и страните се пресичат кръга. Един вписан ъгъл се измерва с половината от дъгата, на които тя разчита.

Централен ъгъл - е под ъгъл, чийто връх се намира в центъра на кръга. Централният ъгъл се измерва с дъгата, на които тя разчита.

Пример 2. точка О - центъра на кръга, ∠ACB = 24 ° (виж фиг.). Вземи ъгъл стойност AOB (в градуси).

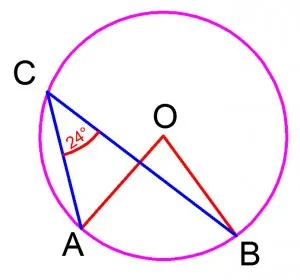
Фигура 14, проблемът на геометрията на кръг от DPA по математика

Решение. АТБ на ъгъл - вписан (връх се намира на един кръг, и този кръг се пресичат страната), тя разчита на дъгата AB. Следователно, от теоремата на вписан ъгъл степен мярка на дъгата AB на два пъти АТБ на ъгъл. т.е. равна на 24 ° · 2 = 48 °.

Други въпроси за ъгъла - център (връх се намира в центъра на кръг), тя разчита на една и съща дъгата AB. Чрез собственост на мярката централната градусов ъгъл е най-малко неговата степен дъга, на която тя се основава, че е ∠ACB = 48 °.

Предизвикателството за независими решения №2. Точка О - центъра на кръга, ∠BOC = 110 ° (виж фиг.). Вземи ъгъл BAC стойност (в градуси).

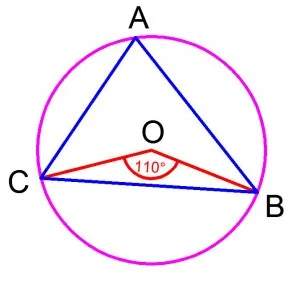
Фигура 14 на проблема с геометрия за независим решението на ДПА в математика

Задача 23 към геометрията на ДПА в математика

Най-трудната задача в геометрията на предложения за ДПА в областта на математиката. Решете се оказва, силите на много малък брой студенти годишно. Независимо от това, да се научат да се реши проблемът 23 от ДПА е по математика е възможно и че е необходимо, дори и само защото тези задачи, които ви очакват в изпита по математика, които също трябва да вземат каквито и да било възпитаници в 11 клас. Подгответе се да отговори на предизвикателствата на геометрията на ДПА в областта на математиката е най-лесно с помощта на преподавател.

Пример 3. страни AC. AB и BC ABC и триъгълник са равни съответно. K точка се намира извън триъгълника ABC. където KC сегмент пресича страна AB в точка различна от В. Известно е, че триъгълника с върхове К. А и С, подобни на оригинала. Намерете косинуса на ъгъла AKC. ако ∠KAC> 90 °.

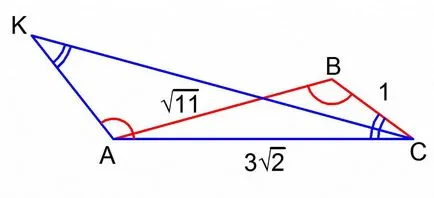
Плановете да се възложат 23 до геометрията на ДПА в областта на математиката

Задачата за независимо решение №3. Страните на триъгълник са 10, 10, 12. Намерете радиуса на вписаните и escribed кръгове.

Това е всичко. Нека си зададем въпроса в края на краищата. Защо имаме нужда да учи геометрията? Не много отдавна аз присъствах на семинар на известния български методист, посветена на методите на преподаване на геометрията в училище. Докладчик в хода на дискусията, между другото, и се задава този въпрос. Отговорът е толкова ми хареса, ще го цитирам тук почти буквално.

Без адекватно хранене не може да бъде нормално развитие на личността. Без разнообразна интелектуална храна не може да бъде нормално интелектуално развитие. Днес, геометрията е един от малкото качествени продукти, консумирани в сферата на образованието. Геометрия - витамин за мозъка. Но в същото геометрията - продукт, който трябва да бъде приготвена много добър готвач. В противен случай, тя не може да донесе само ползи за тялото, но и да му навреди. Така че трябва да научи геометрия на "правилната" преподавател по математика. Само той може да ви помогне да постигнете успех в тази трудна материя. Талантливи учители вас!