Елипса, аналитичната геометрия
Определение 7.1. Наборът от всички точки на равнината, за които сумата от разстоянията до две фиксирани точки F1 и F2 имат предварително определена постоянна стойност, по-нататък елипса.
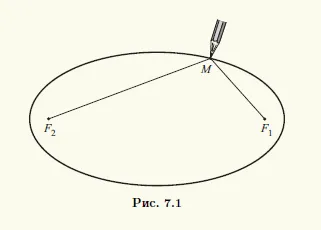
Определяне на елипсата дава следния метод на геометрична конструкция. Ние се определи в самолета две точки F1 и F2. и не-отрицателни константа е обозначен с 2а. Нека разстоянието между F1 и F2 е равна на 2в. Представете си, че неудължаващ низ с дължина 2а, закотвен в F1 и F2, точки. например, с помощта на две игли. Ясно е, че това е възможно само с ≥. Издърпването молива на конеца, направи линия, която ще бъде елипса (фиг. 7.1).
По този начин, описан комплект не е празна, ако ≥ С. Когато а = елипса представлява сегмент с краища F1 и F2 на. и когато а = 0; , Е радиус на окръжността ако споменатото определяне елипса в фиксирани точки съвпадат. Отхвърлянето на тези изродени случаи, ние ще продължим да predpolat, като правило, че> в> 0.
Фиксираните точки F1 и F2 на елипсата в определението на 7.1 (вж. Фиг. 7.1) се нарича огнища на елипсата. разстоянието между тях, определен от 2в, - фокусното разстояние. и сегменти от F1 и F2 М М, М свързващи произволна точка на елипсата с огнища - фокусното радиуси.
Преглед на пълния елипса определено фокусно разстояние | F1 F2 | = 2в и параметър, и своята позиция в равнината - чифт F1 и F2 точки.
От дефиницията на елипсата, следва, че е симетрично спрямо линията, минаваща през огнища F1 и F2. както и на правата линия, която разделя сегмент F1 F2 половина и перпендикулярна на нея (фиг. 7.2, а). Тези линии се наричат осите на елипсата. точка на пресичане O е център на симетрия на елипсата, и той се нарича центъра на елипсата. елипса и точките на пресичане с оста на симетрия (точки А, В, С и D на фигура 7.2, а.) - върховете на елипсата.
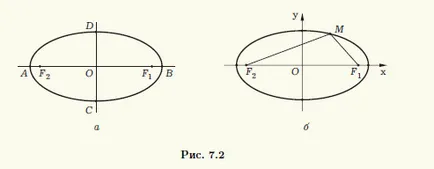
номер се нарича основната ос на елипсата. и б = √ (2 - в 2) - неговата малка ос. Това се вижда добре, че когато в> 0 полуос а е разстоянието от елипса центъра на върховете, които са на същата ос като огнища на елипса на на (пикове А и В на фиг. 7.2, а) и малка ос б е разстоянието от центъра елипса към другите два върха (върховете с и D на фиг. 7.2, а).
Уравнението на елипсата. Помислете за някакъв самолет елипса с огнища на F1 и F2 точки. на основната ос 2а. Нека 2в - фокусно разстояние, 2в = | F1 F2 | 2 + Y 2) + √ ((х + в) 2 + Y 2) = 2а. (7.2)
Това уравнение е неудобно, тъй като тя съдържа две квадратен радикал. Ето защо, ние го превърне. Бързо напред към уравнение (7.2) на втората група от дясната страна, и квадратни на:
(X - в) 2 + Y 2 = 4а 2 - 4a√ ((х + в) 2 + Y 2) + (х + в) 2 + Y 2.
След разширяване скоби и подобни термини задействане получи
√ ((х + в) 2 + Y 2) = а + εx
където ε = с / а. Операцията се повтаря на квадратура за почистване и втори радикал: (х + в) 2 + Y 2 = 2 + 2εax + ε 2 х 2. или предвид въведена епсилон параметър стойност, (2 - в 2) х 2 / 2 + Y 2 = а 2 - с 2. Тъй като 2 - в 2 2 = б> 0, тогава
х 2/2 + Y 2 / б 2 = 1, а> б> 0. (7.4)
Уравнение (7.4) отговарят на координатите на всички точки, лежащи на елипсата. Въпреки това, че произходът на тази уравнение използва неравностойно трансформира първоначалната уравнение (7.2) - Две квадратиране, почистващите квадратни радикали. Изграждането на уравнението на площада е еквивалентно преобразуване ако и двете му страни са ценности със същия знак, но ние не се покажат в техните трансформации.
Ние не можем да се провери съответствието на трансформации, ако се вземе предвид следното. Двете точки F1 и F2. | F1 F2 | = 2в, в равнината определя семейство елипси с огнища в тези точки. Всяка точка на равнината с изключение на точките на сегмента F1 F2. Той принадлежи към семейството на елипса е посочено. В този случай, няма две елипси не се припокриват, тъй като сумата от фокусната радиусите еднозначно идентифицира конкретен елипса. По този начин, на семейството на елипси, както е описано без кръстовища обхваща цялата равнина с изключение на точките на сегмента F1 F2. Разглеждане на множеството от точки, чиито координати удовлетворяват уравнение (7.4) със стойността на параметъра. Може ли това много споделена между няколко елипси? Част от поставените точки принадлежи на елипса с голяма полуос а. Нека този комплект е точка лежи на елипсата с основната ос а. Тогава координатите на тази точка се подчиняват на уравнението
т.е. Уравнение (7.4) и (7.5) имат общи решения. Но това е лесно да се уверите, че системата
ã ≠ известно време все още няма решения. За да се премахне това е достатъчно, например, х в първото уравнение:
че след трансформация води до уравнението
като не решения за ≠ А, като. По този начин, (7.4) е уравнението на елипса с голяма полуос на> 0 и малка ос б = √ (2 - в 2)> 0. се нарича каноничен уравнението на елипсата.
Под формата на елипса. Горният метод за изграждане на геометрична елипса дава добра представа на външната форма на елипса. Но гледката на елипсата може да се изследва с помощта на каноничното си уравнение (7.4). Например, това е възможно, като се излиза от ≥ 0, у изразят чрез х: у = b√ (1 - х 2/2), и се изследва диаграма функция го изгради. Има и друг начин за изграждане на елипса. Окръжност с радиус центрирано в каноничен елипсата координатна система (7.4), описан от уравнение х 2 + Y 2 = 2. Ако компресира с фактор А / В> 1 по ординатата. тогава се получи крива, която е описана чрез уравнение х 2 + (те / б) 2 = а 2 т. е. елипса.
Забележка 7.1. Ако същия кръг компреса с фактор А / В 2 - 2), ε = 2в / 2b = с / б.
Когато с = 0, когато елипсата става кръг, и ε = 0. В други случаи, 0 2 - 2), и а = εa = 4, след това б = √ (5 2 - 4 2) = 3. След каноничната уравнение Тя има форма х 2/5 + Y 2 2/3 2 = 1. за изграждането на които е елипса направи правоъгълник центриран на каноничната опорния кадър, чиито страни са успоредни на осите на симетрия на елипсата и равно на съответните си оси (фиг. 7.4). Този правоъгълник пресича с

елипса оси на върховете А (-5 0), В (5, 0), C (0; -3), D (0, 3), при което се елипсата е вписан в него. Фиг. 7.4 също се фокусира F1,2 (± 4 0) на елипсата.
Геометрични свойства на елипса. Ние презапис първото уравнение в (7.6) във формата на | F1 М | = (A / ε - х) ε. Имайте предвид, че стойността на / ε - х а> век е положителен, тъй като F1 на фокуса не принадлежи на елипса. Тази стойност представлява разстоянието до вертикалната линия D: х = а / епсилон от точка М (х; у), разположена отляво на тази линия. Уравнението на елипсата може да се запише като
Това означава, че този елипса се състои от тези точки М (х; у). (Фигура 7.5) на самолета, за които съотношението на фокусното разстояние F1 М радиуса на разстоянието на ред г е константа, равна на епсилон.
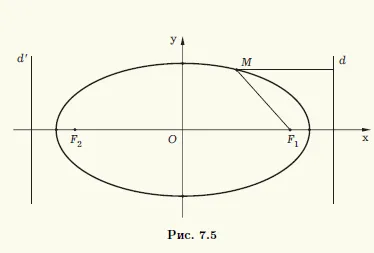
В директен г е "двойно" - вертикална линия г ', г по отношение на симетричен центъра на елипсата, която се дава с уравнението X = S / епсилон. Относително г "елипса е описан, както и относителната г. И двете линии г и г 'се наричат directrices на елипсата. Направляващата на елипсата, перпендикулярна на оста на симетрия на елипсата, на която си огнища и на разстояние от центъра на елипсата и разстояние / ε = A / 2 (вж. Фиг. 7.5).
разстояние Р от директорката на най-близкия до него се нарича фокусно фокуса на параметрите на елипсата. Този параметър е
р = а / ε - С = (2 - в 2) / С = б 2 / C
Елипсата е друг важен геометрична имота: фокална радиуси F1 М и F2 М представлява допирателна към елипсата на равни ъгли на точка М (фигура 7.6.).
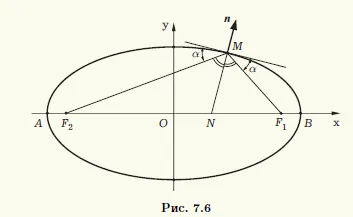
Този имот има ясно физическо значение. Ако фокусът F1 разположен източник на светлина, лъчът излиза от този фокус след отражение от втория елипсата ще фокусно радиус тъй като след размисъл тя ще бъде под същия ъгъл на кривата, както и преди размисъл. По този начин, всички лъчи, идващи от F1 на фокус. ще се съсредоточи по време на второто F2 фокус. и обратно. Въз основа на това тълкуване на горепосочените имоти се нарича оптична собственост на елипсата.