еластични взаимодействия
където Е аз - кинетичната енергия на отделните части на системата.
Фондова стойност П е. равна на произведението на маса М от материал точка на вектора
ν R скорост на неговото движение се нарича инерция на материална точка. т.е. P R = m ν г.
Инерцията на механичната система е вектор сумата от импулси части, съставляващи системата, т.е. P R = Σ P R аз. където Р R I - импулси са части на системата.
Закон за запазване на инерцията е свързана с хомогенността на пространството. В затворена система при липса на външни сили, общата инерция на системата се запазва.
P R = Σ P R I = Σ m и ню R I = конст
Ако стане чрез силата работата зависи от пътя на тялото от една точка до друга, тези сили се наричат разсейване. Примери за това са силите на триене.
Дисипативни сили, ако те са за вътрешна телефонна система, размерът
Когато R R и. р г I - радиус вектори органи и техните импулси. Вътрешните дисипативни сили на големината на ъглов момент не е засегната.
Законите на икономия на енергия и импулс е удобно да учат примера на сблъсъка напълно еластични тела.
Перфектно еластична сблъсък се нарича сблъсък на два или повече органа, в резултат на взаимодействието на органите, без да остави деформации и всички механичната енергия обладан от тялото, за да взриви след удар отново се превръща в механична енергия.
За всяко взаимодействие между две или повече органи на инерция и трансфер на енергия от едно тяло на друго. За перфектно еластично сблъсък закона за запазване на инерцията и закона за запазване на механичната енергия.
В чист вид еластичен взаимодействие се появява в сблъсъка на атомните частици. Ако това не се случи възбуждане на вътрешните степени на свобода на частицата след сблъсък муха без промяна на вътрешната енергия. В сблъсък на макроскопски органи енергийните загуби в резултат на триене и нееластична деформация е неизбежно, обаче, в много случаи, тези загуби са малки, и еластична сблъсък може да послужи като добър модел за изучаване на взаимодействието на реални обекти.
Удобни обекти за изучаване на закони за запазване в механиката са сферични или цилиндрично тяло. Лесен и гъвкав геометрична форма сферична или цилиндрична повърхност го прави лесно да се опише математически сблъсък. В същото време, сблъсък на сферично симетрични обекти често се срещат, например, атомно и молекулно физика.
щифт процес може да се раздели на две фази. В първата фаза след сблъсък органи контакт настъпва компресиране деформация на тези органи, в резултат на което възникват сили, които инхибират конвергенция органи. В тази част на кинетичната енергия на телата той преминава в потенциална енергия на деформация (отчасти в топлина и други видове вътрешна енергия в случай на нееластични сблъсъци). В този момент, на взаимодействащите тела, подобни на компресиран пролетта. След това енергията на деформация на кинетичната реализация, повишаване, докато органите за контакт не престават. След удря еластична тялото възстановява формата си и разпръснете новите ставки. Еластична сблъсък предполага липса на триене.
Разглеждане на еластична сблъсък на две топки или цилиндри на радиуса R 1 R 2 маси m m 2. 1. с начална скорост ν г 1. ν R 2 в отсъствието на полета сила (Фигура 1а.):
След придобиване на тялото сблъсък ф R 1. ф R 2 (фиг. 1b) скорост. експериментален
Това проучване, на пръв поглед, просто физическо явление е трудно, защото Няма лесен измервателни системи за откриване на органите на скорост векторни ценности след реакцията. Математическо моделиране е лесно да се реши този проблем, както и използването на симулация на цялата система от уравнения, описващи явлението,
Тя ви позволява да получите адекватна физическа картина. Законите на опазване на импулс и енергия са (всички третиране е в нерелативистката сближаване)
където m и R и I - маса и вектора позиция на I-точка материал.
Право на движение на центъра на масата: центъра на масовите движения, както в концентрирана маса на цялата система и на която сила е равна на геометричната сума от всички външни сили, действащи върху системата.
Strike нарича централна. ако един удар на тялото да се движи по линия, преминаваща през техните центрове на маса.
Разстоянието между линиите, по които се движат масата на центрове на топки, наречени параметър въздействие делта (Фигура 2)
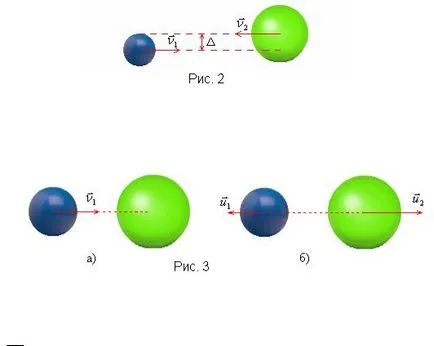
Когато централната еластично тяло снаряд скорост на удара ν R 1 е насочено по централната линия (параметър въздействие Δ = 0) (Фиг. 3a). За простота приемем, че втората топка останалите, т.е. ν R2 = 0.
В този случай скоростите на органите след сблъсъка ф R ф R 1 и 2 също така са насочени по линията
центрове (фиг. 3b), уравнение (7) се осъществява във вътрешната и системата (7) и (8) може лесно да бъде решен. Ние напиши този случай уравнения (7) - (8), разделени от 1 m на предварително:
ν 1 = ф 1 + m m ф 2 2 (9)