еднородна линия уравнение в стабилно състояние - studopediya

Според първоначалните параметри на линията ще разбере съпротива. индуктивност. проводимостта и капацитет. на единица дължина. За хомогенни линия уравнения го разделят на отделни порции безкрайно дължина на структурата, показана на Фиг. 1.

Нека напрежение и ток в началото на такъв елементарен куадруполен са ф и аз. и в края, съответно, и.

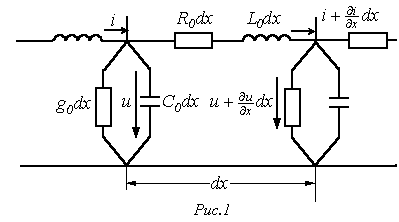
Разликата в напрежението в началото и в края на раздел са определени на напрежението в резистивен и индуктивни елементи, както и текущата промяната в площта е сумата от токовете на утечка и компенсира от проводимост и капацитет. По този начин, според законите Кирхоф

или след намаляване на

;

.

Теория вериги с разпределени параметри, ще се считат за случая на синусоидално ток в стационарни условия. След това получените съотношения на може да се разшири до DC верига, използвайки серия разширяване на Фурие - в линията на периодичната не-синусоидална ток.

Въвеждане на сложни стойности и подмяна. въз основа на (1) и (2) получаваме

;

.

и където - съответно интегрирана устойчивост и проводимост на единица дължина на линията.

Чрез диференциране (3) по отношение на X, и заместване на експресията (4), може да се напише

.

,

.

.

при което - константа на разпространение; - коефициент на затихване; - коефициент фаза.

За текущата съгласно уравнение (3) може да се запише

.

където - характерните импеданс.

Характерните импеданс и размножаване постоянна линия nazyvayutvtorichnymi параметри, които характеризират неговите свойства като устройство за предаване на енергия или информация.

Определяне и. от (5) може да се запише

.

Подобен уравнение съгласно (6) могат да бъдат написани за ток.

Условията от дясната страна на уравнение (7) може да се разглежда като пътуване вълни: първата се движат и се погасява в посока на увеличаване на х, а вторият - намалява. Наистина, фиксирано време всеки от термините, е снабдена (поради загуба на енергия) е хармонична функция на координатната х, и в определено местоположение - синусоидална функция на времето.

Вълните, които се движат от стартовата линия в посока на увеличаване на х, наречена линия, и се движат от крайната линия в посока на намаляване на х - назад.

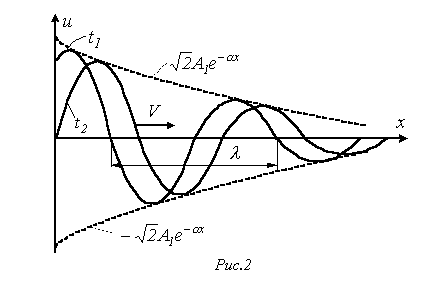
Фиг. 2 е демпферирана синусоида на пряката вълна и за моментите от време. Преместването вълни характеризират с скорост фаза. Тази скорост на движение на линията на постоянно състояние фаза, т.е. скоростта, с която трябва да се движат по линията, за да гледате на същата фаза на вълната:

.

Разграничаване (8) с течение на времето, ние получаваме

.

Дължина на вълната е разстоянието между двата най-близки точки, различаващи се по фаза от рад. В съответствие с това определение,

,

.

В съответствие с понятията, въведени от напред и назад вълните на разпределението на напрежението по линията във всеки един момент може да се разглежда като наслагване на две вълни: напред и назад, - преместване по протежение на линия със същата скорост фаза, но в противоположни посоки:

.

където съгласно (5).

Въвеждане на напрежение като сумата от напред и назад вълни съгласно (10) означава, че положителната посока на напрежение, когато двете вълни са избрани еднакво от горната и долната проводник.

По същия начин, за ток, въз основа на (6) може да се запише

.

Положителните посоки на права и обратна вълна ток, съгласно (11) са различни: положителната посока на директен вълната съвпада с положителната посока на ток (от началото до края на линията) и назад вълна положителна посока е противоположна на него.

Въз основа на (10) и (11), за право и обратно напрежение и ток вълни закона на Ом е доволен

.

Помислете теоретично важен случай на безкрайно дълго равномерна линия.

Безкрайно дълго равномерна линия. Хармонизираният операция

В случай на безкрайно дълга линия в изразите (5) и (6) за напрежение и ток условия съдържат. Не трябва да има, защото желаем да лиши тези компоненти на физически смисъл. Ето защо, в настоящия случай. Така, в решаване на уравненията линия на безкрайна дължина не назад вълна ток и напрежение. В съответствие с гореизложеното

Въз основа на отношенията (12) може да бъде важен извод, че за безкрайно дълга линия по всяко време, включително и на входа, съотношението на напрежение и сегашните системи е постоянна величина, равна на характерните импеданс:

.

Така, ако такава линия психически намали навсякъде, вместо сгънати безкрайно дълго част свързан резистентност е числено равно на вълната, режимът на работа на ограничен период от останалата част непроменен. От тези две заключения могат да се направят:

Уравнения безкрайно дълга линия, намиращ се на линията на крайните дължина, натоварени на съпротивление равен на вълната. В този случай, тъй като има само пряка вълна на напрежение и ток.

В съответствие натоварени на характерните импеданс, входно съпротивление е равна на вълната.

дълга линия режим на работа, заредена с устойчивост, равна на вълната се нарича последователна, а самата линия се нарича линия със съответстваща на натоварването.

Имайте предвид, че този режим е практически важно за предаване на информация, като се характеризира с липсата на отразените (назад) вълни, причинява смущения.

Съответстващо натоварване напълно поглъща силата на вълната, която е достигнала края на линията. Тази власт се нарича естествен. Както във всяка точка на последователна линия на импеданс на вълната е равна, преминаването на ъгъл между напрежението и тока е непроменена. Така, ако силата, генерирана от генератора линия е равна. властта в края на дългите линии в този случай,

,

където ефективност линия

.

Както е отбелязано в това quadripoles, на затихване единица е neper съответстващ поглъщане на енергия във времето, и напрежението или тока - във времето.

1. Bessonov LA Теоретични основи на електротехниката: Електрически вериги. Proc. за студентите от електрически, сила и инструмент специалитети университети. -7 изд. Ревизираната. и вътр. -М. Изпълнителният. седм. 1978. -528s.
2. Теоретични основи на електротехниката. Proc. за средните училища. В три тона., Изд. Ед. K.M.Polivanova. V.2. Zhukhovitsky BJ Negnevitsky IB Линеен електрическа верига (продължение). Нелинейни верига. -М :. Energiya- 1972 г. 200C.
3. Основи на теорията на верига: Учебник. за /G.V.Zeveke университети P.A.Ionkin, A.V.Netushil, S.V.Strahov. -5-изд. Ревизираната. -М. Energoatomisdat, 1989. -528s.

Контролни въпроси и задачи

1. Каква е разликата между веригите с краен и параметри?
2. Какво е верига критерий принадлежи към класа на вериги с разпределени или същинските?
3. Начертайте смяна верига дълга линия.
4. Обяснете на концепцията за напред и назад, пътуващи вълни.
5. Това, което е договорено операция верига с разпределени параметри, които характеризират той?
6. Определяне на параметрите първични линия, ако вторичните параметри.

1. Определяне на условията на предходната задача линия ефективност дълги 200 км, като се има предвид, че той е поставен на съпротивата, равна на вълната.

1. Определете. и кабелна които имат. , ако честотата.

1. Съгласно условията на предишния проблем да се определи дължината на вълната и фаза скоростта.