Дискретна математика алгоритми
Описание на цифровата комуникация процес
Източник издава съобщение, което представлява най-общия случай на определен електрически сигнал. Този сигнал се преобразува в цифрова форма, която е подходяща за по-нататъшна обработка.
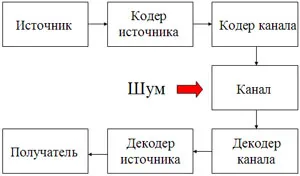
След това е компресия на данни (кодиране източник), минимизиране на излишъка на съобщението. кодиране източник намалява разходите за предаване и съхранение на информация. Посланието трябва да бъде предадена на шумна канал. За че съобщението достигне до потребителя в ненарушена форма, като се използва безшумен кодираща информация (канално кодиране). На информацията за потребителите страна се декодира. декодер коригира грешки в получената дума, и декодер източник преобразува коригира думата във форма, удобна за потребителя.
Говорейки за кодовете, които контролират грешките, ние трябва да се прави разлика между две стратегии за тяхното използване.
- за поправка на грешки в резултат на съкращения (Forward Error Correction - FEC).
- откриване на грешки и последващите искания за препредаване на неправилно получена информация (автоматично повтаряне заявка - ARQ).
При избора на кодиране и декодиране методи се ръководят от много фактори, връзката което е представено на фигурата.
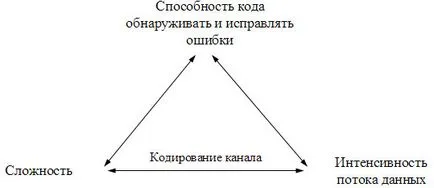
Общата сложността на хардуер и софтуер, са разходите за изпълнение на енкодер и декодер, съхранението и разходи за излъчване и така. Г. поток интензивност данни включва предаване на полезна информация битовете за контрол, а също така иска и изисква повторение на тези индивидуални информационни блокове.
безшумен кодиране
Преглед
Реалното предаване на данни система не е съвършена. Прилагането на информационните технологии, ние трябва да се разгледа възможността за грешки при предаването и съхраняването на информация. Това главно се отнася до
- съхраняване на информация върху среда за запис с висока плътност (магнитни носители, CD-ROM, DVD);
- прехвърляне на данни на по-ограничена мощност на сигнала (сателитни и мобилни комуникации);
- предаване на информация в силно шумни канали (мобилна комуникация, високоскоростен жични връзки);
- канали за комуникация с високи изисквания за надеждност информация (мрежи, електропроводи с компресиране на данните).
Във всички по-горе случаи, се използват кодовете, грешки контрол.
Помислете за най-простите данните модел, използвайки за корекция на грешката кодиране.
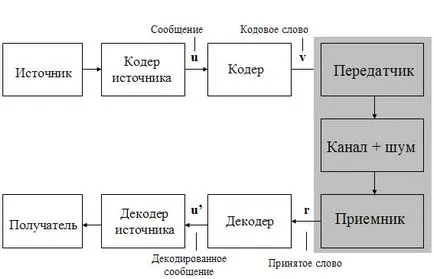
Да предположим, че източник на енкодери последователно изходи фиксирана дължина думи за данни. канален енкодер замества всяка кодова дума данни дума Ф Х. Предавателят генерира сигнали, съответстващи на кодова дума V и го изпраща на канала. Приемникът извършва обратна трансформация, в резултат на което декодера получава получи двоична дума R. Декодера сравнява получената дума R с всички кодови думи използва кода. Ако думата а съответства една от кодовите думи, съответстващи на информационната дума, и издаден на потребителя. Ако R е различен от всички кодовите думи, тогава той открива е станала грешка в канала. С цел прилагане на кодиране на канала е да се постигне съвпадение на предадената информация думата ф и получената информация думата ф ".
От това описание е възможно да се направи 2 O:
- Ако в процеса на прехвърляне на шумна канал кодова дума ще се появи в различна кодова дума, която не съвпада с преминалата, нещо се случва неоткриваем грешка. Ние я наричаме остатъчен декодиране на грешката.
- Задължително за изграждане на кодове, които имат някаква математическа структура, която може ефективно да се открие, а в някои случаи и за коригиране на грешки при предаването на информация по комуникационен канал.
Linear Блокиране на кодове
Важен семейството на кодове образуват линейни двоични блокови кодове. Тези кодове са забележителни с това, че, представяне на информация и кодови думи под формата на двоични вектори, ние можем да опишем процесите на кодиране и декодиране с помощта на апарата на линейна алгебра. Така компоненти на входните вектори и матрици са символи 0 и 1. Операции с двоични елементи са произведени в съответствие с правилата на аритметиката модул 2.
Най-добре познатият линеен код е блок код Хеминг а. Допълнително описание на линейни блокови кодове ще се извърши на един пример за кода. По-специално, тя ще се счита (7,4) -code Хеминг.
Binary блок енкодер (н. K) -code показва множество 2 к възможни битови информационни думи в множество от двуизмерен к н кодови думи. В теорията на кодирането между тези набори винаги е кореспонденция едно към едно.
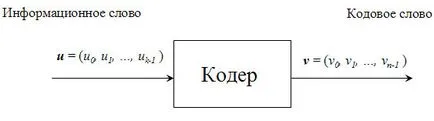
Вместо к-битова информация вектор в п-битов канал предава код вектор. В този случай се говори за прекомерно кодиране със скорост: R = п / к.
Колкото по-ниска е скоростта, толкова по-голяма резервираност и толкова повече възможности за грешка, което има. Въпреки това, трябва да се отбележи, че увеличението на разходите за пренос на ненужната информация също се увеличава.
Описание на процеса на кодиране и декодиране
Структурата на пространство код вектор
Изходният материал за изграждане на конструкции код служи като двоичен п двумерен вектор пространство, където посочените аритметични операции модул 2. вградени к двумерен вектор пространство, съдържаща 2 к кодови думи. код С се формира от комбинациите от 2 к к линейно независими базисни вектори
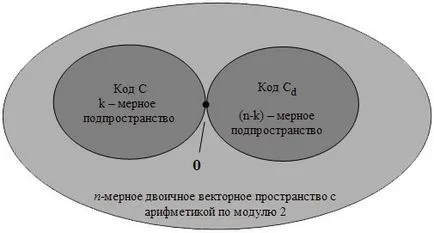
Тези вектори образуват редица от матричен код на генератора В.
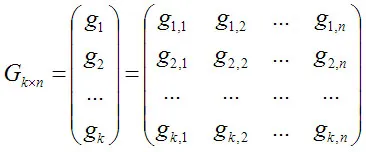
Има двоен код С г до С код, така че скаларен продукт от всяка двойка вектори, един от които принадлежи на С, а другият - пространство С г. Той винаги е нула. Това означава, че кодът на векторите С г ортогонална вектори код В. От друга страна, ако вектор е перпендикулярна на всички вектори на код C, че той принадлежи към код С г и обратно. Dual вектор подпространство "обтегнати" в п - к линейно независими базисни вектори
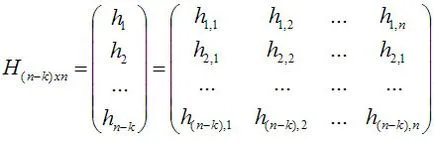
Помислете например за генериране на матрицата за проверка и (7,4) код на Хеминг:
Трябва да се отбележи важно свойство, както в генерирането и матрицата за проверка присъства идентичната матрица. Това свойство се използва в процеса на кодиране и декодиране.
кодиране
Кодова дума срещу и информационната дума, ф са свързани с:
където G - матрица поколение. структурата на който е описано по-горе.
Например, информация вектор ф = (1010) се показва във вектор код, както следва:
Лесно е да се забележи, че през последните четири бита на код вектор съвпадат с информацията за вектора. Това свойство се нарича системен код.
Кодове, които дума данни могат да бъдат предоставени директно от съответния codevector той нарича систематични. Генериране на матрица на всеки системен код винаги е възможно, чрез прегрупиране на колоните към формата:
където к - на идентичност матрица с размер к х к.
По този начин, в код вектор системното код винаги може да се подчертае информация и проверка символи.
V 0 ... о п - к -1
о п - к ... о п -1
п - к паритет
к информационни символи
Роля на паритет и тяхното използване ще бъде обяснено по-подробно по-долу.
декодиране
Decoder задача е да, с помощта на код структура на полученото дума R. възстановяване на предаваната информация вектор. Обсъдено по-горе за (7, 4) код Hamming може да предложи следния алгоритъм за откриване на грешки. Тъй като се счита кодът е систематичен, експресират всеки от трите символи паритетни чрез информация вектор:
Ако е възникнала грешка в канала, приетия вектор R поне ще се извършва една от уравнения. Пишем получените проверка отношения в система от уравнения за компонентите на вектора г.
Така първите три колони на генератор матрица G, ние получаваме система от три уравнения проверка. Ако най-малко един от компонентите в получената система от уравнения не е нула, една грешка в канала.
Пишем проверка за четност уравнения в общата форма. За всеки системен код с генератор матрица G. проверка матрица се определя, както следва:
Н (п - к) х п = (I п - к Р Т к х (п - к)).
След това системата за валидиране на уравнения може да се запише като
вектор те се нарича синдром. По този начин, грешката ще бъдат открити, ако поне един от компонентите S не е равно на нула.
Като пример, помислете за Синдром на декодиране (7, 4) код на Хеминг. При предаване на информация дума ф = (1010) по канал без шум R = V = (0011010). Можем да видим, че в този случай, този синдром е 0.

Ако, например, в кодовата дума имаше една единствена грешка на четвърта позиция (R = (0010010)), този синдром е четвъртият ред на транспонирана проверка матрица.
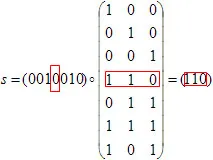
След като става чрез всички възможни позиции на единична грешка, ние получаваме пълна маса на синдроми грешки единични - таблица съответства на броя на неправилно освобождаване се получава от този синдром.
Може да забележите, че грешката в аз-тата позиция в кодовата дума съответства на синдрома формира от -тата колона от Н. матрица От всички колони са различни, ние можем да използваме таблицата на синдроми да се коригира една единствена грешка, въведена от канала.
сортове грешки
За линейни блокови кодове, има 3 вида грешки:
- Разпознава и корекции на грешки
- Получени дума не отговаря на някое от кодовите думи
- Синдромът е в таблицата на синдром
- Декодера открива и коригира грешки, а след това предава на приемника правилната дума
- разпознаваем грешка
- Получени дума не отговаря на някое от кодовите думи
- Синдромът е в таблицата на синдром
- Декодера открие грешка и изпраща заявка за препредаване на думата на данните.
- Непризнат грешка
- Получени дума съвпада с една от кодовите думи (не съответния оригинален кодовата дума)
- Синдромът е 0
- Декодера не може да открие грешка, и извежда на потребителя погрешна информация съобщението
заключение
Трябва да се отбележи, че ефективността на даден код в зависимост от областта на приложение и по-специално от комуникационния канал. Ако канал съотношението S / N е достатъчно голям, вероятността от единична грешка е много пъти по-висока от вероятността от грешки по-високи поредни, следователно, използването на такъв Hamming код за канал за коригиране на грешки единични може да бъде много ефективно. От друга страна, в канали контролирани от множество грешки (например, избледняване канали), корекция единична грешка е безсмислено. В практиката да се избира специално за корекция на грешката код е необходимо да се помисли за неговата скорост на декодиране и сложността на техническото изпълнение.
литература
Единственото ясно обяснение!
Наистина ясно обяснение, което едва ли може да се намери. благодаря
Трудно е да се разбере книгата, вижте момчетата