Директен равнина и Euclidean геометрия

Няколко хиляди математика, опитващи се, от една страна, за да докажат, пети постулат на Евклид, но, от друга страна, се чудя, защо го е добавен в първите четири Евклид.

Пети постулат винаги е бил смятан излишни.

Един от неговия текст гласи - "На равнина през точката, която е права линия, можете да рисувате само една права линия, успоредна на това."

Спомнете си, приета от Евклид определения и свойства:

Определението за "точка е, че той все още няма части" Оттук следва, че въпросът е отсечка, чиято дължина е равна на неговата ширина. Следователно, въпросът е част от по-прав или частен случай на ред на дисплея, а в същото време, неговата дължина и ширина не са равни на нула, тъй като в този случай точката не съществува;

Определението на "Директно има такава линия, която е еднакво до всички точки" на горната дефиниция, че по права линия - равнина, чиято широчина е равен на ширината на точката.

Следователно, по права линия - равнината част или конкретен случай равнината на дисплея;

Определението на "повърхност равнина, която е еднакво за всички директно върху него лежи" означава, че самолетът може да се състои от точки, линии или други линии равнини съвпадат с това.

От това следва, че самолетът е основната концепция, и точката, и линията е специален случай на самолет.

Продължавайки да се твърди в същия дух, ще получим бунтарски мисълта, ако основната концепция се състои от отделните случаи, самото понятие трябва да представлява специален случай.

В планиметрия Лобачевски-Бояй през точка извън линията на самолета може да побере произволен брой различни линии паралелно с това. Това е - аксиома.

В планиметрия Риман през точка извън линията не може да побере всяка линия, успоредна на тази. Това твърдение също axiomatized. Тя ще изглежда, че може да бъде подривни в тези аксиоми? Къде може да е неточна, която в продължение на толкова много години объркани много учени? Неточности се крие в една дефиниция, и това определение - концепцията за "равнина".

Постулира това определение, като абсолютен самолет, ние се намираме в един нереален двуизмерен свят на Барон Мюнхаузен.

В реалния триизмерния свят - Самолет е повърхност с радиус на кривината клони към безкрайност.

Това означава, че е налице пряка линия, която е една и съща за всички точки на повърхността с определен радиус на изкривяване.

Радиусът на кривата на самолет, а с него и линията може да бъде всеки и определени от специфични той сили, действащи в самолета в района на кривата в процес на разглеждане, а не правоъгълна.

Следователно, реалната точка, имаща дължина, ширина и дебелина е извита повърхност. За да опровергае това, опитайте се да намерите прав участък на повърхността на кръг или сфера.

Може би това е, което се поставя под въпрос в геометрията му на Евклид, въвеждане на геометрията пети постулат. Пето постулат прикрепен Euclidean равнина свойства напълно плоска повърхност. Въвеждане на понятието кривина показва евклидовата геометрия от плоска двуизмерна свят на нереалното за реално триизмерен свят на кривата.

Двуизмерен абсолютно плосък евклидовата геометрия става специален случай, при условие че радиусът на кривината на разглеждания самолет или кривата клони към безкрайност.

В момента на Евклид, най-вероятно не е имал представа за кривината на пространство и дори самата Земя се гледа като на идеално равна повърхност.

Въпреки това, Евклид вероятно не са съгласни с това определение.

Изявление по това време, че земята е извита повърхност, или повече топката не биха били тълкувани правилно.

Вероятно, петата му постулат на Евклид изпрати "загадъчен съобщение" за бъдещето на човечеството, което показва, че геометрията му с равнина не всичко е наред, че тя е измислил - хипотетично, неговият пети постулат.

Постулира абсолютна равнина, Евклид даде човечеството способността да се създаде удобно и лесно да се прилага: геометрия, математика, физика, и по този начин се положат основите за скок в безкрайната шир на извитата пространство.

Признаване на факта на невъзможност за съществуването на абсолютна равнина, това вероятно е в основата на създаването на нови геометрия, физика, математика, както и по пътя на знанието на Вселената.

Науката обаче все още е правоъгълен триъгълник Питагор, построен на абсолютна равнина евклидовата геометрия на, е в основата на международно признати теории, описващи структурата на Вселената.

Вземете Лоренц ги превърне в стойността √ 1 срещу 2 / C 2, получен от Питагоровата правоъгълника.

Това е в противоречие с буквата и духа на теорията на кривината на пространство. в който няма място плосък правоъгълен триъгълник, идеално прави линии и перфектно гладка повърхност.

Отново си спомни Евклид и си точка определение.

"Въпросът е, че който няма части." В реалния свят, въпросът е геометрична тяло.

Постулатите на Евклид не казва нищо за дебелината на точката.

В реалния свят, че не може да посочи за да представи най-малкия кръг с липсващи дебел.

Ако добавим към определянето на условията е също неговата дебелина, а след това той трябва да бъде най-малката топка.

В този случай, ние не можем да се възползваме от плосък триъгълник на Питагор не разполагат с дебелина.

На точка купа, като ако не се намали неговия размер, правоъгълен триъгълник ще има три прав ъгъл и този триъгълник не ще бъде в състояние да се превърне в плоска.

Пренебрегването втори ред малка стойност, когато триъгълника е заменена с извита повърхност на правоъгълна, плосък триъгълник в микросредата води до огромни грешки.

Провеждане на изчисленията за повърхности траектории, чиято кривина радиус клони към нула, ние получаваме че клони към нула област триъгълник Euclidean и Lobachevskian стойности величина от втори ред, т.е. области на разликата или дължини в тези геометрии, поема стойност леко Тя не е равно на квадратните триъгълници или разстояния между точки.

Лесно е да си представим, че тази разлика е достатъчна, за да се изгради опростен модел (Фигура 1) двуизмерния Euclidean триъгълник в триизмерен Lobachevsky триъгълник.

Площта на триъгълник ABC Lobachevskian S = 4 πR 2/8 = 2/2 πR

Square Euclidean триъгълник, правоъгълник, изчислен въз основа на Pythagoras S ABC = R2√3 / 2

Тъй като, ако R не са склонни към нула, разликата е равна площ на триъгълник и на триъгълника на топката ще бъде различен за:

Игнориране на тази разлика и да приемем, че тази неточност магнитуд от втори ред, които не могат да се вземат под внимание, очевидно не е вярна.

Същото се случва и с пътя на движение на точка А от безкрайност до нула - точка В, където радиусът на кривината клони към нула (Фигура 2).

В частта, където R → ∞ (фиг.2) AB крак, ако ние прилагаме правоъгълния триъгълник Питагоровата хипотенуза практически еднакви и влизаме в Нютоновата физика

В сегмент AB, където R → 0 (Фиг.2 дясно) крак AB трансформира в дължина L. акорд, който се изчислява по формулата:

L 2 = а (2 R - а).

Сключването на тази формула показва още vIIIveke в китайската книга "Математика в девет книги" в проблема с индийски matematikaVIIveka Bramagupty на.

Описание на траекторията на електрона и неговото въртене на базата на реални триизмерни криви и обема на триъгълници. а не на базата на двуизмерен многоъгълни прави и плоски правоъгълници позволяват математици да попаднат вътре в атома, и разкриват тайните на неуловим пространство.

Признавайки безценния принос на физиците, които са работили до третото хилядолетие, ние трябва да признаем, че те не са в състояние да дешифрира тайните послания на Евклид, предвидени от тях в пети постулат.

Модел на материята и пространство, създаден въз основа на правоъгълна правоъгълник на Питагор, трябва да признаем, двуизмерен.

Третото хилядолетие трябва да бъде едно хилядолетие на рамка, която описва реални триизмерни модели на изкривено пространство и материя.

Пети постулат на Евклид 3 D пространство.

Представлява пети постулат на Евклид като цяло в триизмерното пространство.

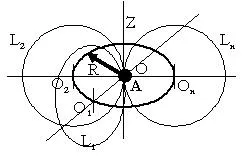
Чрез (фиг.3), дадена равнина O1. с радиус на кривина, с тенденция към безкрайност, с центъра O1. направи линия L 1, с радиус на кривината тенденция към безкрайност и съвпада с центъра на кривината O1 равнина.

Преместване в центъра на кривината на върха O2. и през точката А, принадлежащи към линия L 2. O2 равнина. с центъра на кривината O2 равнина.

Както можете да видите направо L 1. L 2. не се пресичат в една обща точка А.

По този начин е възможно да се проведе безкраен брой паралелни линии L 1. L 2. ..., L п → ∞ не принадлежат към дадена равнина, но като обща точка А, при условие, че координатите на центъра на кривина O1 на всяка равнина. O2. ..., G п → ∞, описват окръжност на радиуса на кривината R → ∞ около оста Z.

В ос Z е най-често срещаните допирателни равнини за всички взети под внимание.

В този случай ние се получи триизмерна форма част от тор, с равнопоставеността на R. Като цяло, R може да бъде отличен стойност.

В реални, физическо пространство, радиусът на кривината не е безкрайна, но ограничена сила, определена от физичните свойства на среда и реакционна среда счита областта на други области. Тези свойства причиняват деформация на равнината на огъване като радиусът на всеки и всички негови оси на симетрия.

От пети постулат на следните условия:

1. Координати Z равнина, и следователно пряко и определени условия като принадлежащи към равнината са равни.

2. Един от X или Y координата определя от точки, които не принадлежат към линията.

3. Директно има само една степен на свобода.

4. В центъра на кривина на линия, успоредна на дадена само една ос може да бъде преместен да се съобразят с паралелизъм.

Следователно, пети постулат на Евклид, е специален случай, който описва единственият изход от безброй.

В самолета с предварително определен радиус на кривина през точка, която е права линия. можете да рисувате само една права линия, успоредна на тази, в която поне една от координатите на центъра на кривина не съвпада с координатите на центъра на оригиналния кривината.

Тази интерпретация пети постулат обикновено описва пространствен тръба (Фигура 4) с радиус на кривината R → ∞.

Въвеждането на понятието кривина в описанието на самолета и прави, води до парадоксален извод:

Всеки ред, с безкрайните си продължаване на затворена крива.

В действителност, ако по права линия е радиусът на кривина, това означава, че има кръг, който се образува, независимо от радиуса, до безкрайността.

Следователно кривата направо не начало и край.

Curve, с произход от безкрайност и си проправиха път, krutanuvshis на безкрайното пространство, отново отива до безкрайност.

Като една права линия могат да бъдат разграничени едни от други?

Ако вземем координатите на началото и края на линията, а след това те са несигурни безкрайност.

И ако сравните радиусът на кривината на "Директно"?

В този случай, ние веднага ще бъде в състояние да се разграничат един ред от друг.

В реалния физически свят, всичко, разбира се. Оттук и радиуси на кривина на "преки" и "равнини" са ограничени.

Означава ли това, за крайността на нашата Вселена?

В крайна сметка, според строителния геометрията на модела на кривата се оказва, че ако се преодолее равнина с радиус на кривината клони към безкрайност е възможно да се стигне до подземния свят. Въпреки това, по начина, по който ще се срещне непреодолима абсолютно прав, допирателна към кривата.

Идеално права линия в истинската природа не съществува (вж. По-долу).

По принцип "нарисува" геометрия, колкото е възможно.
Това е достатъчно, за да се възползват от геометрията на Риман.
Въпреки това, възниква въпросът тук.
Възможно ли е да се движат в тази геометрия?
В този случай, трябва да признаем, че има центробежни ускорения, т.е. движението на ускорението има отрицателен радиус на кривината вектор.
Реалното физическо движение се случва при прилагането на принципа на импулсното захранване (IS) в мащаб надвишава размера на силата на реакцията поле вълна, действаща на инерционно тялото в състояние на покой.
Възниква въпросът.
За някои път, има движение под влиянието на Е.
Чрез центробежен или центростремителна?
Този въпрос е от значение, че отговорът на това определя коя геометрия трябва да се използва, за да опише траекторията.
Ако това центростремителна движение, траекторията на кривата трябва да бъде описан от действителната геометрия на Лобачевски. Това означава, че в центъра на кривината е в рамките на вписан кръг.
Ако това центробежни движение, траекторията на движението трябва да бъдат описани въображаеми криви Риман геометрия. Това означава, че в центъра на кривина се намира извън вписан кръг.

Помислете например за движението на ракетата по време на ускорение.

По време на стартирането на стартовата на радиуса на кривината на траекторията на ракета е равен на радиуса на Земята R Н на (фиг.5).
Както е известно, по време на ракети ускорение тя остава в орбита около Земята, ако не и първата космическа скорост е надвишена.
Това, от своя страна, означава, преобладаването на центростремителна сила на гравитационното напрегнатостта на полето, генерирани глобус.
Траекторията на ракетата време на това движение с центростремителна радиус на закръгление R на езерото насочена към Земята. При достигане на скорост бягство ракетата надхвърля действието на гравитационното поле на Земята.
Означава ли това, че траекторията на ракетата стана центробежен?
Отговорът е очевиден - не.
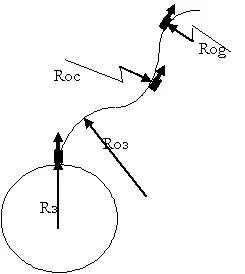
В този случай, траекторията на ракетата определя гравитационното поле на Слънцето. Траекторията на ракетата в този центростремителна лявата, но с радиус на кривина R OC насочена към слънцето. Това означава, че тя се променя само позицията на центъра на кривина.
Същият резултат получаваме, като се има предвид трета космическа скорост, с която ракетата лети по радиус на кривина на рог. В центъра на това място радиуса от центъра на галактиката определя т.н.
По този начин, като се има предвид в който и да е движение, не можем да намерим естеството и вида на центробежните сили.
Признаване на съществуването на центробежна сила води до признаването на съществуването на задгробния живот и възможността за движение на един въображаем път, който противоречи на съществуването на реалния свят.
Освен това, за да премине от Евклид геометрия, с реални радиус R. Риман геометрия с въображаем радиус - Р. бъдат преодолени напълно прав, допирателна към кривината на което се стремим права линия с безкраен радиус на кривина R Фиг.6.

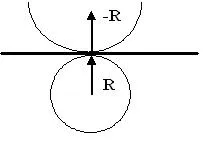
За преодоляване на допирателната в движението преход от реалното към въображаем Lobachevskii геометрия на Риман геометрия движението на извита центростремителна първо трябва да се превърне в един абсолютно права линия, и едва след това да влязат в един друг свят - извита центробежни движения.
Но това е абсолютно линейно движение предполага абсолютна равнопоставеност на сила действие на опозиционните сили, който отрича възможността за всяко движение.
Това е вероятно да има геометрична доказателство за липсата на центробежната движение.
Но, както е отбелязано по-рано, движението идеално права тангента, не съществува. Това означава, че материята, пространството, в този случай да изчезне, защото изчезват всички сили.

F = Силата на действието - реакционната сила = 0

Въпреки това, преобладаването на мнение в научния свят за съществуването на центробежните сили е довело до факта, че всички оси в прилагания математически апарат са с посока от центъра на фигура 7, която е една въображаема линия, а не в центъра, за реалното - действителната посока на фигура 8.

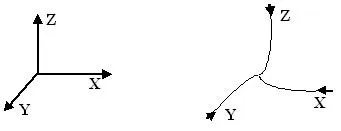
Фигура 7 Фигура 8
Въображаемият, прави, криви, недвижими
ос координатни оси

Това води до значителни грешки в математическото описание на материята, пространството, както и записани природни явления.
Извитата пространство, по време на движение по крива траектория, осите си трябва да са криволинейни, Фиг.8.
Определение.
Физическо движение напред е движението на вълните, околната среда, тялото, материята на центростремителна траектория с кривина насочено към действието на силите на съпротивата.
радиус кривина Център движение физическа постъпателно, от вътрешната страна на извивката, смята парцел траектория.
Въз основа на изложеното по-горе, може да се предположи, че изпълнението на заветната мечта на човечеството - летят в неограничено пространство при условие, трябва да отидете на траекторията на ракета с радиус на кривината клони към безкрайност, което е близо до абсолютно права линия, свързваща две точки в пространството.