Диференциални уравнения в общия диференциали 1
Определение 8.4. В диференциално уравнение на формата
където
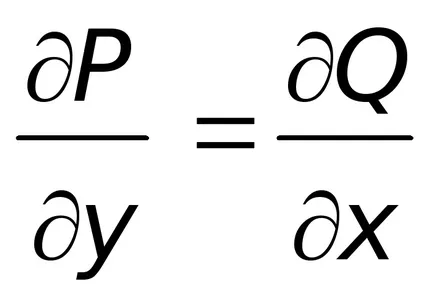
Имайте предвид, че от лявата страна на това уравнение е общата разлика на функция
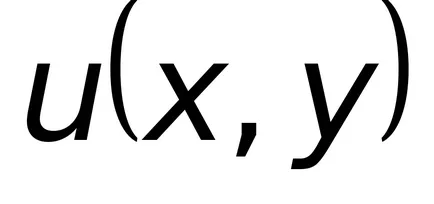
В най-общия случай, уравнение (8.4) може да се запише като
Вместо уравнение (8.5) може да се счита уравнението
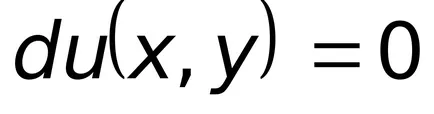
решение, което има общо интегрално уравнение (8.4). Така разтвор на уравнение (8.4) е необходимо да се намери функцията

функция
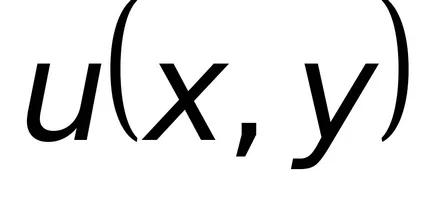

където


функция
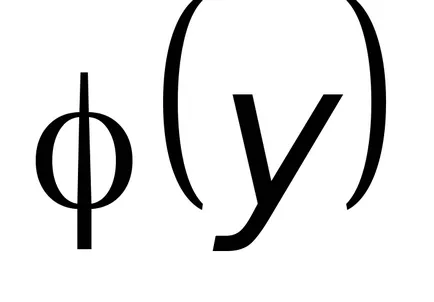
От израза (8.7) и се определя от функцията
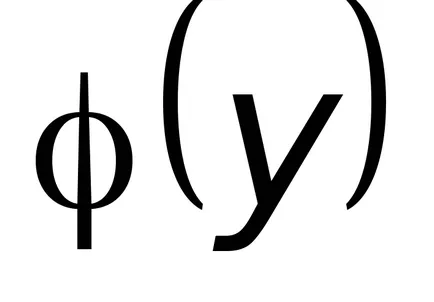
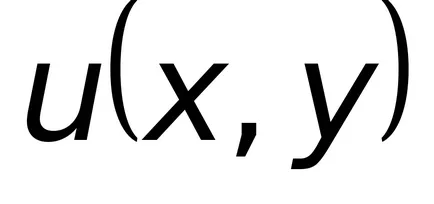
Задача 8.3. интегриране на уравнението
Следователно, уравнението е от диференциални уравнения тип в общия разлики. функция
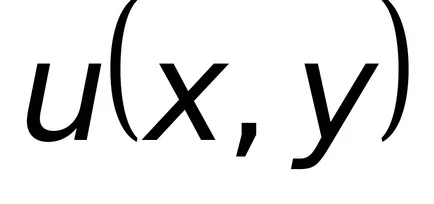
;
;
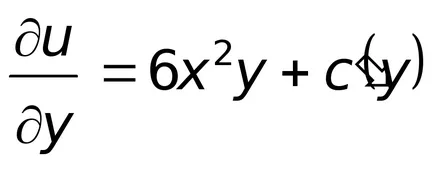
От друга страна,
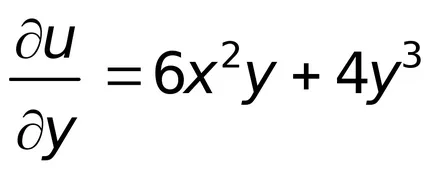
.
В някои случаи, при условие
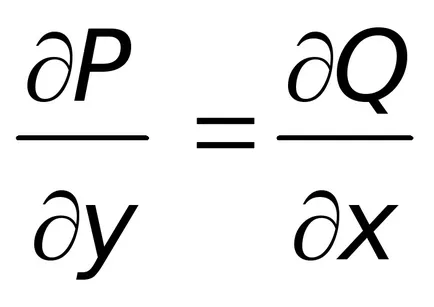
Тогава тези уравнения за разглеждания тип се множат от т.нар интегриращ фактор, който по принцип е само функция


Ако има интегриращ фактор в уравнение, което зависи само от

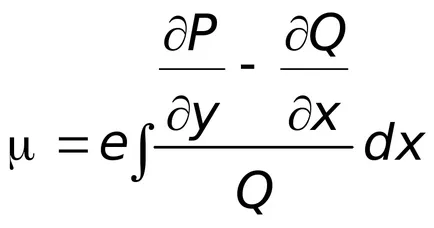
където съотношението на


По същия начин, интегриращ фактор, който зависи само от

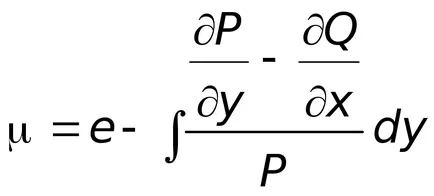
където съотношението на
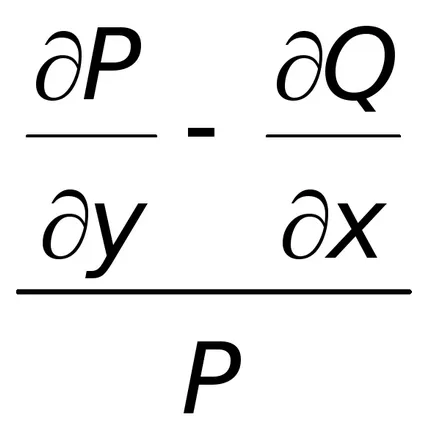

Липсата на горните съотношения в първата променлива например


Задача 8.4. Довежда уравнението на уравнение с обща диференциал.
.

.

Тема 8.2. Линейни диференциални уравнения
Определение 8.5. диференциално уравнение
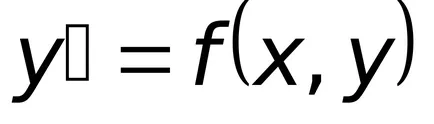


Общата форма на линеен диференциално уравнение е представена със следната зависимост:
Ако съотношението (8.8) от дясната страна
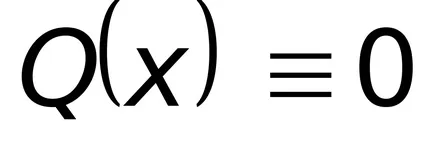
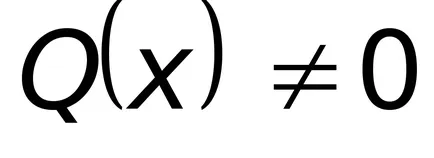
Нека покажем, че (8.8) е интегриран в квадратури.
В първия етап считаме хомогенна линейно уравнение.
Това уравнение е уравнение с много променливи. В действителност,
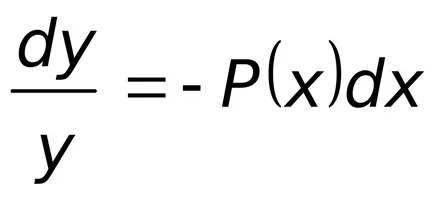
;
/
Последният връзката определя обща хомогенен разтвор на линейното уравнение.
За общото решение на нехомогенни линейното уравнение метода на вариант на производно константа. Идеята на метода е, че общото решение на нехомогенни линейното уравнение в същата форма като тази на хомогенен разтвор на съответния уравнение, но произволен постоянен


Заместването в уравнение (8.8) изразът съответстващ
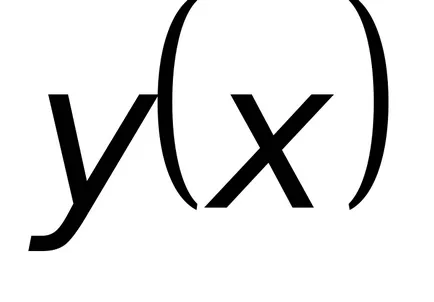
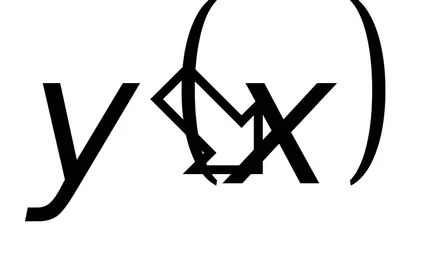
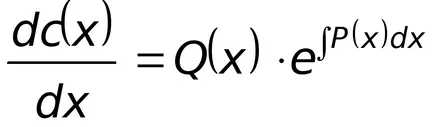
Заместването последната експресията в (8.9), давайки общо неразделна линеен нехомогенни уравнение.
По този начин, общото решение на нехомогенни линейно уравнение, определена от две площ: общото решение на линейно уравнение хомогенна и конкретен разтвор на нехомогенни линейното уравнение.
Задача 8.5. интегриране на уравнението
Следователно, първоначалното уравнение е от типа хетерогенна линейни диференциални уравнения.
В първия етап ние намерим общо решение на линейни хомогенни уравнения.
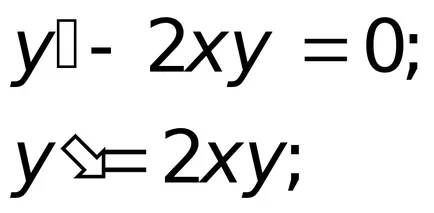
;
На втория етап се определи общото решение на нехомогенни линейно уравнение, които търсят взети под формата
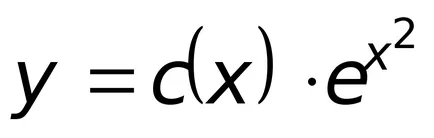
където
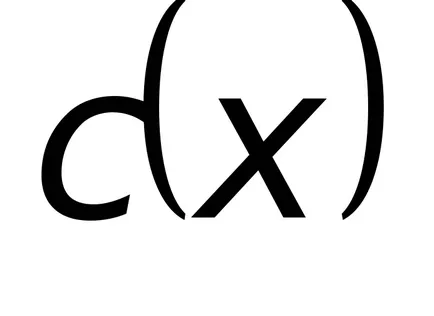
Заместването на


;
;

Общият разтвор на нехомогенни линейното уравнение ще бъде:
