Броят на оборота в единица време е реципрочен на периода

Лесно е да се получи връзката между ъглово и линейно точка на скорост.

Когато се движи по член дъга от окръжност, свързани с отношението безкрайно въртене. Тук.

да я поставите в (1), откриваме, че линейната скорост на модула е равна на

С формула (4) се отнася големината на ъгловите и линейни скорости.

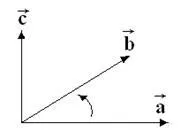
По-обща връзка е видно от чертежа, където вектор линейна скорост е вектор продукт на ъгловата скорост - и радиус вектор точки:

1. Вектор proizvedeniemvektorov наречен вектор, чиято големина е равна на площта на успоредник, образуван от коефициента на вектори и собствени вектори и образуват дясна вектори.

2. Вектори ,,> образуват дясна ръка, ако най-краткия въртенето на вектора на вектора, се вижда от крайна точка вектор може да бъде генериран в посока "стрелка".

Ъгловото ускорение - е време производно на ъгловата скорост (или втори път производно на ъгъла на завъртане)

3. Примери за изчисляване на кинематични характеристики на превозното средство.

раса автомобил се движи в разрез прав път, така че нейните ускорение нараства линейно през първите и 10с достигне стойността 5 m / и 2. Пренебрегването своя размер и тегло, за да се определи края на 10-секунди: скорост 1) на превозното средство; 2) преминава по пътя си.

Както ускорение увеличава линейно, и неизвестен коефициент на пропорционалност - м / сек.

Чрез хипотеза движение - праволинеен, а оттам и скоростта -

Изминато разстояние праволинейно движение ще бъде равен на:

1) с формула (1) - м / сек; 2) с формула (2) - м.

Track модел превозно средство връзват върти с честота Hz. След прекратяване пръти, модел, което прави завои, спря. Пренебрегването на собствената си размери и тегло на модела на колата, определи ъглово ускорение - ако се приеме, че инхибирането е ravnozamedlennym.

Тъй като инхибиране ravnozamedlennym прие, ъгълът на въртене -

където ъгловото въртене честота, Hz (2).

Крайната стойност на ъгъла - Rad (3).

Крайната стойност на ъглова честота - по този начин отношението - където времето на спиране на (4).

Заместването в уравнение (1) връзка (2), (3), (4), ние откриваме, че рад / C.

Забележка. Разтворът може да се получи в общ вид, като се предполага, че определени общи изрази - (2 ÷ 4). Тогава рад / в.