атомната физика

Смисълът на квантово число: това е един по-малък от броя на нули на вълновата функция. константата

Тя се определя от състоянието на нормализиране.

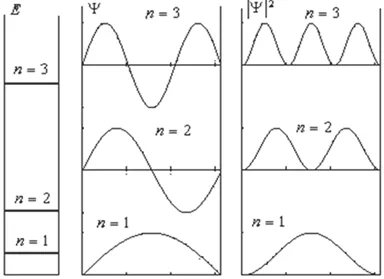
Фиг. 4.8. енергийни нива, функции вълна и вероятностно разпределение плътност по х координират

Имайте предвид, че стойностите, за които граничното условие на мястото, също ще бъдат извършени, новите страни не са разрешени. Това личи от израза за енергията (4.24), в който п е включен в кутията, а от израза за вълновата функция (4.25): п смените знака само ще доведе до промяна в вълновата функция на марката, че ще остави непроменена вероятностно разпределение.

Къде дискретни нива на енергия, характерни за атома? Сравними с безплатна частиците: уравненията са едни и същи, но с различни гранични условия! Има две възможни форми на проблема. В първия случай се изучава състояние, което в класическата механика, ще съответства на безкрайно движение (разсейване проблем). Обикновено в такива случаи, разтвори са възможни при всички стойности на енергията (както се казва, спектърът е непрекъсната). Във втория случай състоянието е изследвано, което съответства на класически ограничен движение в ограничена област на място (на проблем, свързан състояние). Изисквания на края на вълновата функция в цялото пространство води до енергийна квантуване. Стрес: в този случай равновесно състояние уравнение е физически приемливи решения не винаги, но само в определени енергии. Като следствие, отделен енергиен спектър на системата.

Пример. Ние дефинираме разликата между съседните нива на енергия за частиците в безкрайно дълбоко потенциал и за големи стойности на п. Резултатът, получен с помощта на разликата за оценка на енергията на съседна енергийни нива на транслационно движение на молекулите на азот при стайна температура в съда. Да приемем тегло на молекулата, и линейни измерение на плавателния съд. Ние сравняваме резултата с кинетичната енергия на постъпателно движение на молекулярен азот.

С помощта на уравнението (4.24) за енергийните нива на частица в потенциална добре, разликата в енергиите намираме съседните нива

за големи стойности. Средната кинетичната енергия на транслационно движение на молекулите на азот е

Приравняването на изразите (4.24) за енергийните нива на частиците в кладенеца, ние откриваме, че такава енергия квантовата съответства на номерата за поръчка

Сама по себе си тази цифра показва, че в областта на много високи възбужденията тече класически формула. Разликата в енергия между съседните нива се получава чрез заместване на формулата за изразите намерени номерата на квантовата:

електронни волта същите характеристики са както

относителната енергийна разлика между съседните нива е пренебрежимо:

и тъй като в класическия граница на квантовата стъпки пренебрегвани.

Частици в триизмерен потенциал добре

Това е обобщение на предходната проблема. Частицата може да се движи в кубичен обем с дължина на ръба. Лесно е да се провери, че общото решение за вълновата функция може да се представи като произведение от едномерни вълнови функции, получени през предходната задача:

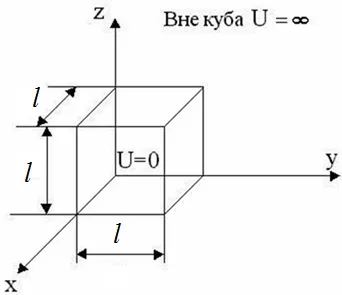
Фиг. 4.9. Триизмерно потенциал добре

състояние на системата в момента се определя от три квантови числа 1. 2 и 3. Решението, както преди; целочислени стойности. Тук за първи път се сблъскват с важната концепция на дегенерацията на енергийните нива, т.е. ситуация, в която различните състояния на системата имат една и съща енергия. В действителност, на минималната енергия на системата се постига с минималните стойности на всички квантови числа, това е, когато 1. 2. 3. Тази енергия е

и съответства на функция вълна. Говори се, че основното състояние не се изродят (nondegenerate държави с минимална енергия - общото правило). Първият възбудено състояние се получава, когато един от квантовата числа равни на 2, а другите са все още равен на един; своята енергия

Но толкова много власт сега имаме три състояние на функциите на вълните, и (квантово число 2 може да бъде избран по три начина), така че те казват, че израждането на първи развълнуван ниво е три (г = 3). Естествено, различна система може да бъде съвсем различна дегенерацията (или липсата на такава). След държавния частиците в триизмерен потенциал добре с безкрайните стени също така се изроди. Ясно е, че дегенерацията на нивата поради симетрията на системата, с равни права за всички оси. Ако размерите на ямата са различни 1. 2. 3, че и трите части, енергията, която би трябвало вместо (4.27), изразът

и дегенерация ще се случи само при определени съотношения между дължината, ширината и височината на потенциалната кутията.

В класическата физика пружина махало (двумерен осцилатор) е маса m точка тяло, пружина и свързан към вибриращо с ъгловата честота. Потенциалната енергия на системата е описано от

така че уравнението на Шрьодингер в писмена форма

От тук можете да се намери решение за вълновата функция на основното състояние

Замествайки този израз в уравнението на Шрьодингер е лесно да се види, че енергията на основното състояние е равно на

Ние не пиша функциите вълна на възбудени състояния на осцилатора, но изразът за допустимите стойности на енергията се получава от (- вибрационно квантово число)