5) Метод еквивалентни трансформации
При изчисляване на сложни електрически вериги в много случаи, е целесъобразно да ги направи опростяване чрез коагулация чрез заместване на някои части на веригата със серийни, паралелни NYM и смесени съединения съпротивления с един еквивалент на устойчивост-валентна по метод, еквивалентни на предварително образувания (метод преобразяване) вериги.
. А) електрическа верига с последователно свързване на съпротивления (Фигура 1.2.1) се заменя с верига с един еквивалент soprotivleniemRekv-валентна (Фигура 1.2.2), равна на сумата от всички съпротивления верига:., Където - Устойчивост индивидуален верига порции.
P
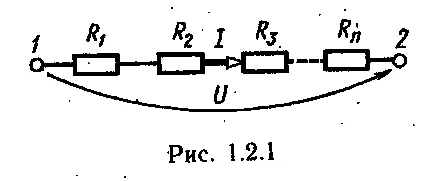
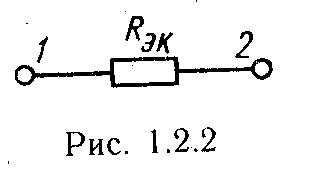
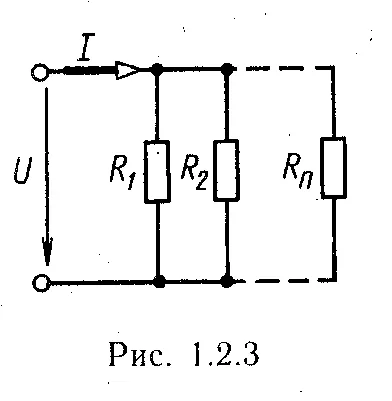
б) В паралелни съпротивления връзка придружава всички съпротивление при същия napryazheniemU (Фиг. 1.2.3). Електрическата верига, състояща се от съпротивления, свързани паралелно, е целесъобразно да се замени с еквивалентно верига soprotivleniemRekv (Фиг. 1.2.2) се определя от експресията-желаят да се създаде
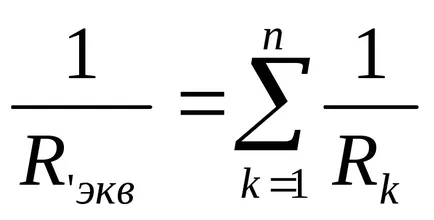
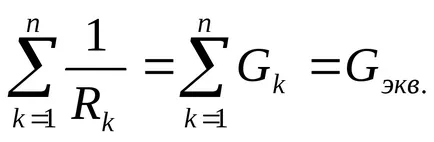
сумата от реципрочните на съпротивленията на порции клонове паралелно-ционни верига (сумата от клоновете на проводимости верига); RK - устойчивост на паралелната част верига; Gekv. . - еквивалентната проводимост на паралелната част верига Gekv = 1 / Rekv п - брой паралелни разклонения верига. съпротивление верига участък еквивалент, състояща се от идентични Paral взривоопасни свързани съпротивления, Rekv = R / п.
в
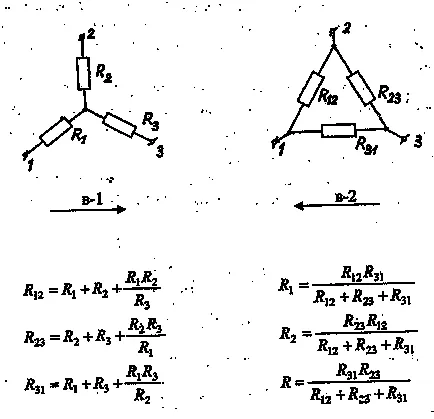
6) пропорционален метод (определяне) количествата

Вземете електрическата схема на фиг. 3.1 Tocache Обърнете произволна стойност на съпротивлението R6, най-отдалечените от доставката. За дадена устойчивост на текущата R6 определи напрежение. На следващо място, ние определяме:
, ,
, ,
; ,
Ние считаме, EMF
.
Получената стойност на EMF е различен от едн предварително определена стойност Е. изчисли коефициента на сходство. Умножете го получава чрез изчисляване на стойности на токове и напрежения, намират самите течения ценности верига.
7) Метод за изготвяне на цялостна система от уравнения на Кирхоф
Във всеки електрическа верига в съответствие с първия закон на Кирхоф алгебрична сума от течения насочени към възел е равно на нула:

В съответствие с втория закон на Кирхоф алгебричната сума е. г. а.
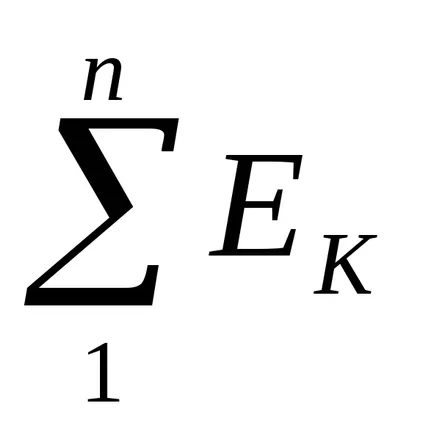
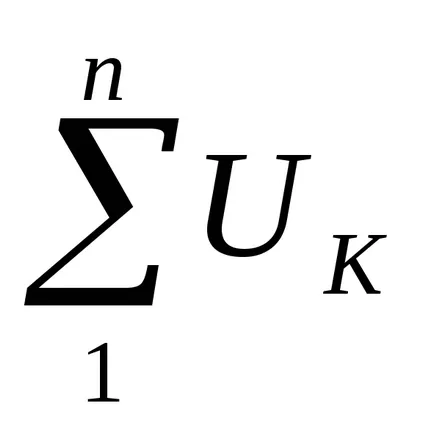
При изчисляването на електрически вериги чрез прилагане Kirchhoff Зуко ново избрани условни положителни посоки на токове и напрежения на верига секции EMF които означават стрелките на диаграмата, след това затворен контур и са принудително посока байпас вериги. Тук, за удобство на посоката изчисление на преминаването на всички вериги се препоръчва да се избере една и съща (например, по часовниковата стрелка).
Когато се избират уравненията на втория закон на Кирхоф за електрически вериги, съдържащи източници на ток затворени контури, без източници на ток. За неза висими-уравнения е необходимо всяка нова верига включва поне един нов клон, които не са включени в предходните контурите, които вече са били записани в второто уравнение Зуко, добре Kirchhoff.
Броят на уравнения, съставени от втория закон на Кирхоф, необходими за изчисляване на електрическата верига е равен на броя на неизвестни Н.
В повечето случаи, параметрите EMF източници или-конюгиране, източници на ток, резистори RE сайтове изч известни верига, броят на неизвестни е равна на време-ност между броя на клоновете и броя на източници на ток N = (NB-NT). За да се опрости изчисленията, първо напиши просто уравнение, състоящ се от правото на първата Кирхоф и изчезналите - втория закон на Кирхоф.
Броят на уравнения, съставени от първия закон на Кирхоф, е взето е един по-малък от броя на възлите в Ню Йорк верига на:
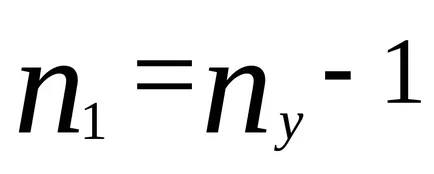
Други брой уравнения
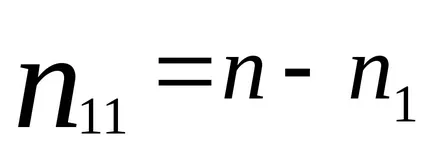
Когато уравненията на втория закон на Кирхоф източници на ЕМП са получили положителни, ако посоката на стъпките им съвпада с избраната посока на цикъла на преминаването, независимо от посоката на тока в него. Когато nesovpade-SRI им запис със знака "-". Спадът в напрежението в клоните, където положителна посока ток съвпада с посоката на байпаса, независимо от източник на напрежение в посока на тези отрасли - със знак "+". В противоречие на спада посока-на празен ход напрежението е написано със знака "-".
С решаването на получената система от п уравнения са валидни области, определени стойности в съответствие с техния знак. Стойностите, които имат отрицателен знак, всъщност, са с посока, обратна на условно прието. Посоки променливи, които имат положителен-тия знак съвпадат с конвенционално приета посока.
разтвор в резултат системата уравнения за да се определят неизвестните количества. Стойностите със знака "+" в действителност имат посока, която съвпада със съответния първоначалната схема да се уточни условно-ми посока. Стойностите със знака "-" в Дебит ефект имат посока, обратна на първоначалната условно предварително определена посока е показано на диаграмата.