19 грунд за
§ 19. право на пречупване на светлината
Съотношението на синуса на ъгъла на падане на синуса на ъгъла на пречупване е постоянна и равна на относителната пречупване между две среди.
Когато светлината достигне интерфейса между две прозрачни медии, част от него се усеща и остатъка преминава през границата. На пречупване на светлината е промяната в посоката на разпространение на светлината, тъй като преминава през границата между две среди. Обяснете пречупване на светлината, например, че един молив потопени под наклон в една чаша вода ни изглежда счупен, а долната му част е изместен (вж. Фиг. 19а).
Пречупване на светлина се дължи на факта, че в различни среди светлината изминава при различни скорости. Ние откриваме колко посоката на разпространение на светлината с помощта на принципа на Хюйгенс ". Да предположим, че Z0Z равнинна връзка между две среди (1 и 2) попада плосък светлинна вълна, съдържащ две успоредни греди и A0A V0V. и вълна повърхност AL A0A съответства на честотата на лъча на границата (фиг. 19Ь).
За вълната повърхността на светлинна вълна предава от средно 1 до 2 среда (на пречупен вълна), плик определи вторични вълни в средата 2. възникващи в места на падане на Z0Z повърхност. Тъй като AL - перпендикулярна V0V. След това, както е показано на фиг. 19б. вторична вълна в точка А настъпи по-рано, отколкото в точка Б в интервала от време
където c1 - скоростта на светлината в среда 1. Поради това, когато V0V лъч. Z0Z достигане на повърхността. в среда 2 ще доведе до вторична вълна, вълна средно центриран в точка А достига точка К и радиус става равна на
където с2 - скоростта на светлината в среда 2. След тези две конструкции за междинните светлинна вълна лъчи, и се намира между A0A V0V. лесно да се изгради полукръг, съответстваща на повърхността на вълната на вторичните вълни в същото точката от време (вж. пунктираните линии и полукръговете на фиг. 19Ь). Според принципа KB тангента Хюйгенс на вълната повърхности на тези вторични вълни на повърхността на вълната ще бъде пречупен светлинните вълни.
В Ъгълът между пречупен лъч и нормалата към АА1 Z0Z. наречен ъгъл на пречупване. Фиг. 19Ь показва, че
където п - константа, наречена относителен индекс на пречупване. Така, съотношението на синуса на ъгъла на падане на синуса на ъгъла на пречупване е равно на константата на двете среди - относителна индекса на пречупване. От конструкциите направени на фиг. 19Ь показва, че инцидента и пречупени лъчи, както и перпендикуляра към намалената честота точка, лежат в една равнина. Двата предишни отчети заедно представляват закона на пречупване на светлината.
относителна Индексът на пречупване равен на съотношението на светлината скорост в средата 1 до стойност в средата 2 (виж фиг. 19.1). Ако средата е един вакуум, индекс на пречупване, който се изчислява по формулата (19.1), която се нарича абсолютна индексът на пречупване на среда 2, N2. които, очевидно, е винаги по-голям от 1. От (19.1), че изразът е валидна за всеки две медии:
където N1 и N2 - абсолютен пречупващи индекси 1 и 2. среда с по-малкия абсолютен пречупване, наречени по-малко оптично-гъста.
Според (19.1-19.2) при честота на лъча от оптично-малко плътна среда на по-плътен, например, от въздух към вода, ъгълът на пречупване е винаги по-малък от ъгъла на падане (вж. Фиг. 19Ь). Обратно, когато лъчът се движи от по-оптично гъста до по-малко плътна среда, ъгълът на пречупване е винаги по-голям от ъгъла на падане (фиг. 19с). Въпреки това, тъй като ъгълът на пречупване не може да надвишава р / 2, това означава, че ако б # 972; lshih пречупена греди ъгълът на наклона ще бъдат липсват. Това явление се нарича пълно вътрешно отражение, и като лесно се показва, това се случва, когато
Пълно вътрешно отражение се случва вътре леки водачи. в състояние да предава светлината на дълги разстояния.
Прегледайте въпроси:
· Формулиране на закона за пречупване на светлината.
· Когато е налице пълно вътрешно отражение на светлината?
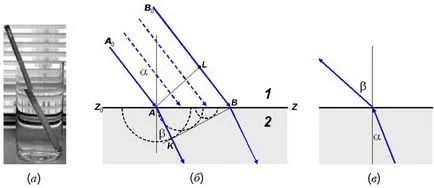
Фиг. 19 (а) - илюзия счупен молив спадна във вода; (B) - сключването на закона за пречупване на светлината; (C) - движението на светлинния лъч на повече оптически плътна среда на по-малка плътност.