03_Ryad разпределение
Вероятността за единица равна на 1/6. Както при всеки друг брой точки. Вероятност за запис на най-долния ред. Редица разпределението направено.
Случайни velichinaH- редица гербове в хвърлят две монети.
Когато хвърли две монети можем да видим poyavleniedvuh гербове, герба на една или няма. Вероятностите на всяка от тези стойности, изчислени от класическата дефиниция. За да направите това, пишем всички възможни резултати и да ги брои:
Компанията е сключила две сделки. Вероятността, че първият ще донесе по-големи печалби ravna0,6. 0.8 секунди.
Случайни velichinaH- брой високо печеливши сделки.
Възможните стойности на случайна променлива: 0, 1ili2.
За изчисляване на вероятностите на тези ценности трябва да използвате формулите на събиране и умножение на събитията.
Ние описват събитията, чиито вероятности са известни за нас:
Изчисляваме вероятността на всеки от възможните стойности на случайната променлива:
P (X = 0) = Р (А B) =<независимы>= 0,4 0,2 = 0,08;
P (X = 1) = Р (А B + A B) =<слагаемые несовместны,
Ние всичко тласък на масата и да получите броя на разпределение
Аналитичен представяне на редица разпределение
Понякога не мога да пиша отделно всеки вероятност и zadatodnu обща формула, за които се изчисляват вероятностите за всички възможни стойности на случайната променлива.
В този случай, все още nuzhenspisok znacheniysluchaynoy възможни стойности:
И формула за изчисляване veroyatnosteykazhdogo до него се добавя:
Редица разпределение комплект.
Графично представяне на някои разпределение
сяка възможна стойност на случайната променлива има вероятност на появяване. Т.е. характеризиращ се с чифт номера
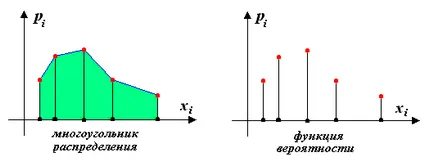
Този начин на представяне на редица разпространение са, за да се получи ясна представа кои от възможните стойности на случайна променлива се появява по-често и които по-малко.
Как да разбера, че законът на разпределение на случайна променлива с които да се работи?
В много случаи това udaetsyapostroit от теоретични съображения, както и в примерите по-горе.
Znacheniyasluchaynoy Възможните стойности се определят въз основа на условията на експеримента, фактът, което се счита за случайна променлива.
Veroyatnostipodschityvayutsya класическото определение или с помощта на формули за сумата и произведението на събитията.
Ако теоретично изграждане на броя на разпределение е невъзможно, информация за него може да бъде получена чрез поредица от наблюдения на случайна променлива и извършване на обработката на статистически данни. Как се прави това, ще научите izuchayamatematicheskuyu статистика.
В примерите, всеки път, когато посочените по-горе, ако добавите всички вероятности в редица дистрибуции, получаваме 1.
Ние perebralivsevozmozhnye опции. Т.е. събития obrazuyutpolnuyu група. Освен това, onipoparno несъвместими (в един експеримент, случайна променлива отнема само една стойност). Според теоремата оказа по-горе, сумата от всички вероятности трябва да е равна 1.
А сега погледнете как mozhemispolzovatryad разпространение, ако го има.
Ако броят на разпределение, установен, ние mozhemprognozirovatpovedenie случайна променлива.
Тъй като е случаен, ние не знаем колко е важно да се вземе в следващия експеримент.
Но ние mozhemrasschitatveroyatnosttogo че ще интересен стойност, ще си дойде на интеграл от интерес за нас.
На въпрос редица разпределение.
Изчислява вероятността случайна променлива се предварително определена стойност:
е вероятността, че случайна променлива X ще се стойност, равна на (-4). Но това може да отнеме само стойностите, посочени в таблица :( 2, 5, 7, 11). Така случай (X = - 4) - невъзможното, и вероятността е нула:
.
Изчислете вероятността случайна променлива ще падне в определен интервал от време:
е вероятността, че случайна променлива X заема стойност по-малко от (-2) .Such стойности тя не.
Това може да се случи, ако това ще отнеме стойността. равна на (2) ..
Това може да се случи, ако това ще е от значение. равна на (7) или (11). (само тези две възможни стойности са по-големи от или равни на (6)).
По този начин, на събитието (X6) може да се представи като сума от две взаимно изключващи се събития:
.
Следователно, вероятността на това събитие е:
Аргумента, всеки път, по същия начин, стигаме до извода, че за дискретна случайна променлива вероятност да изпадаме в някаква площ, равна на сумата от вероятностите на възможните стойности, които попадат в тази област:
ох
