03 Лекция
Целта на преобразуването на електрически вериги.
Ясно разграничаване на порции с серийни и паралелни връзки, когато се обмисля смесен окабеляване.
За да можете да конвертирате съединение в еквивалент триъгълник звезда и обратно.
За да можете да конвертирате източник на напрежение в източник на ток и обратно.
схеми за преобразуване схеми.
За превръщане на електрически вериги, е опростяването им, е необходимо за по-голяма простота и удобство на изчисление.
Един от основните типове електрически вериги превръщане е вериги преобразуване съединение смесени елементи. Смесени свързващи елементи - комбинация от серийни и паралелни връзки, и който ще бъде разгледан в началото на тази лекция.
Фиг. 3-1 показва клон верига, при което съпротивлението R1 са свързани в серия. R2, ..., Rn. Чрез всички тези съпротивления преминава същия ток I. Напреженията на отделните части на веригата се означава с U1. U2, ..., Un.
Фиг. 3-1 серия връзка.
Тъй като напрежението в клон на ZNK
Съпротивлението на всички части от този бранш

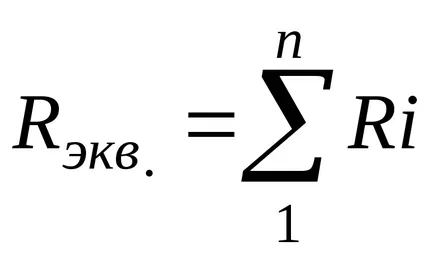
Тя се нарича еквивалентно съпротивление серия.
Тъй като напрежението, което пада върху отделните съпротивления, тези съпротивления са пропорционални, може да се каже, че серийно свързване на съпротивление образуват "делител на напрежение". Концепцията за делител на напрежение се използва широко в практиката.
Фиг. 3-2 показва схема на две възли, между които са включени п успоредни клонове с admittances G1. G2, ..., Gn. Напрежението между възлите U, то е едно и също за всички отрасли.
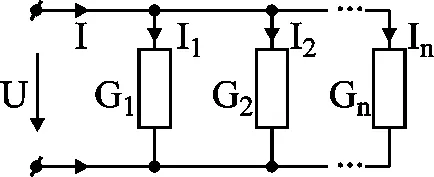
Фигура 3-2 паралелно свързване (показан трансформира).
Според общото NTA е сумата от токовете на отделните отрасли:
Сборът от стойностите на проводимостта на всички отрасли, свързани в паралел
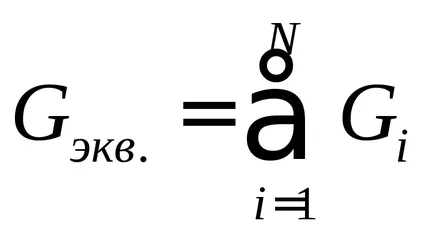
Тя се нарича еквивалентен проводимост.
В случай на паралелно съпротивление на два клона (п = 2) обикновено използвани изрази, които включват устойчивост
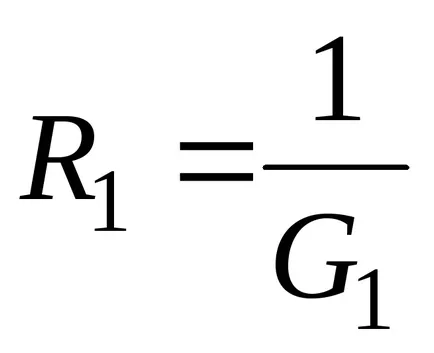
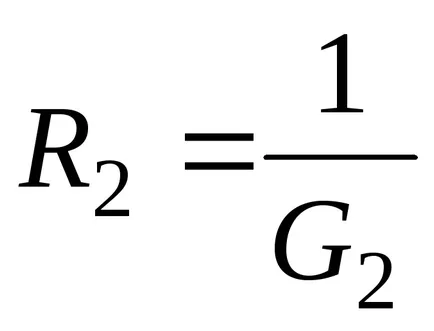
Еквивалентната съпротивлението на две паралелни свързани клонове е:
Тъй като общият ток е разделена на отделни клонове на токове пропорционални на проводимостта на тези клонове (или, еквивалентно, е обратно пропорционална на съпротивлението на тези клонове), може да се каже, че съпротивлението на паралелно свързани, образуват "делител токове". Концепцията за текущия разделител се използва в практиката.
Често, когато с помощта на "ръчно" изчислителни вериги трябва да се определи колко ток се разделя над отделни клонове на паралелните връзки клоните.
От формула (2), че настоящите клонове, свързани паралелно, е пропорционален на проводимостта на тези клонове, т.е. токове са разделени по клоните, пропорционални на съпротивлението на тези отрасли, или, което е същото, е обратно пропорционална на съпротивлението на тези отрасли.
В случай на две паралелно свързани устойчивост на общото съпротивление (2) е:
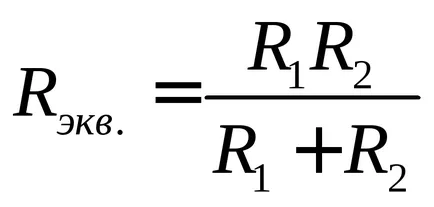
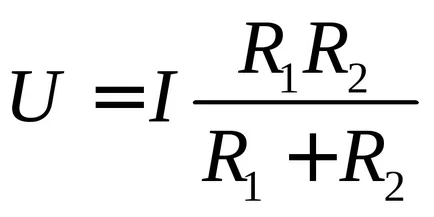
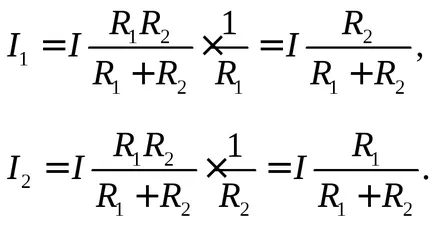
Получените изрази за токовете понякога се нарича "правило рамо", който гласи ток е разделена между успоредните свързан резистори (ток делител) е обратно пропорционална на тези съпротивления.
На Фигура 3-3 показва смесен съединение електрическа верига:
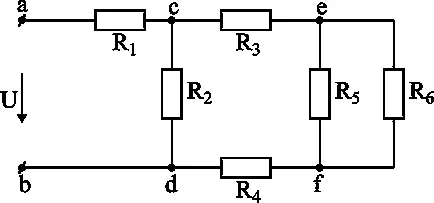
Фигура 3-3 смесена съединение.
Тази схема е лесно да се намали до една единствена верига. Устойчивост R5 и R6 са свързани паралелно, така че е необходимо да се изчисли еквивалент устойчивостта на частта от формулата

могат да бъдат представени чрез междинен рамка за разбирането на резултатите, получени (Фиг. 3-4).
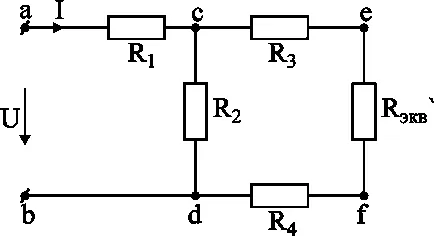
Устойчивост R3. R4 и R / екв. свързани в серия, еквивалентно съпротивление част и С-E-F-D е равно на:
След тази фаза трансформация е под формата на диаграма на фиг. 3-5.
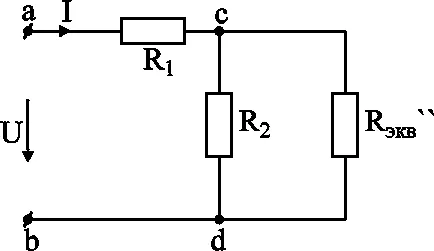
След това откриваме еквивалент съпротивлението на част C-D и сумира с съпротивлението R1. Общият еквивалентно съпротивление е равно на:
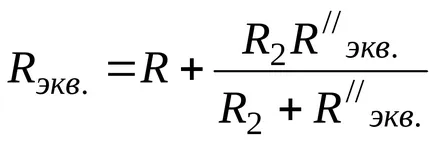
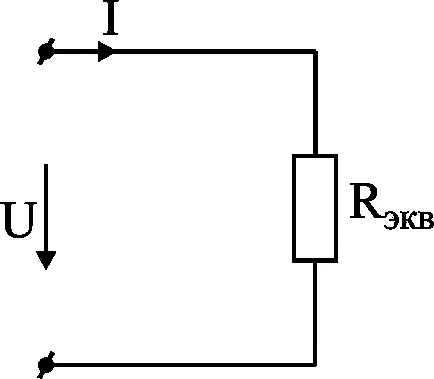
Получени резистентност еквивалент резистентност (Фиг. 3-6) от първоначалната схема смесен съединение. Терминът "еквивалент" означава, че напрежението на входните U и ток I вход клон терминали остава непроменено за всички трансформации.
Преобразуване на триъгълника спрямо еквивалентния звездата.
Превръщането в еквивалентно звезда триъгълник определена да бъде резервна част верига свързан делта, верига, свързани в звезда, при която токове и напрежения в останалата част от веригата, остават непроменени.
Т.е. триъгълник равностойност и звездите означава, че по едно и също напрежение между едни и същи терминали течения, включени в заключенията на едно и също име са едни и същи.
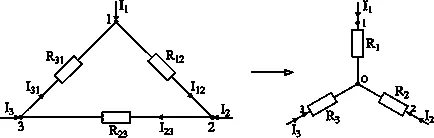
Фиг. 3-7. Преобразуване на триъгълника в звездата.
Нека R12; R23; R31 - устойчивост страни на триъгълника;
R1; R2; R3 - устойчивост на звездата;
I12; I23; I31 - течения в клоновете на триъгълника;
I1; I2; I3 - токове подходящи за терминали 1, 2, 3.
Ние изразяваме токовете в клоновете на триъгълник в съответните пунктове за ток I1. I2. I3.
По закон, напрежение сума от пада на напрежение в триъгълника на контур на Кирхоф е равна на нула:
Според закона на Кирхоф от токове на възлите 1 и 2
В решаването на тези уравнения за i12 получи:
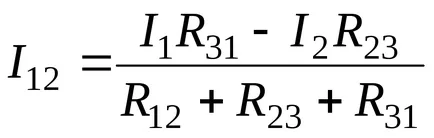
Напрежението между точки 1 и 2 от схема триъгълник:
Напрежението между едни и същи точки на схемата на звезда е:
защото е еквивалентна превръщане, е необходимо равенство на напрежения между точките от данните на двете вериги, т.е.
Това е възможно, ако:

Третият експресията получава чрез заместване на кръглите индекси.
Въз основа на експресията (5) формулира следното правило:
Устойчивост лъч звезда е продукт на съпротивата на страните на триъгълник, в непосредствена близост до гредата, разделена на сумата от съпротивлението на триъгълника три страни.
Преобразуване звезди в триъгълник еквивалент.
При преминаване от звезда на триъгълник са известни съпротивление R1. R2. R3 на звезда. Стойностите на съпротивлението на триъгълник се определя от Обединеният разтвор от уравнения (5):
Страната на устойчивост на триъгълника е сумата от съпротивленията на съседните точки на звездата и техните произведения, разделени от съпротивата на третия лъч.
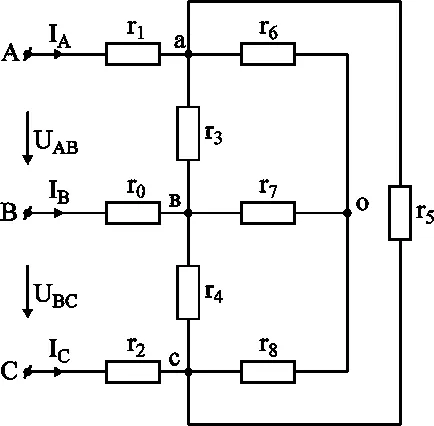
Решение: Resistance R6. R7. 8 образуват една звезда;
R3 резистентност. R4. R5 образуват триъгълник.
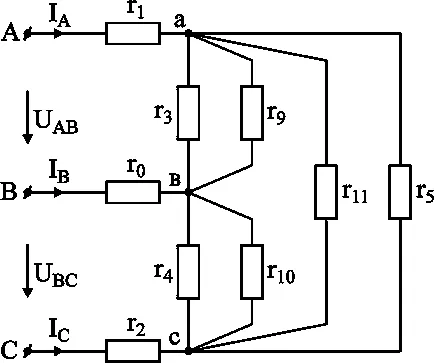
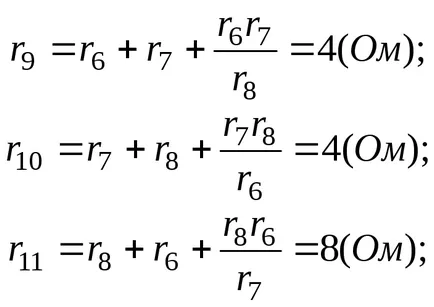
В резултат на преобразуване получи два триъгълника с успоредни страни (фиг. 3-9). Намираме еквивалентните резистентност страни на триъгълника (Фигура 3-10).
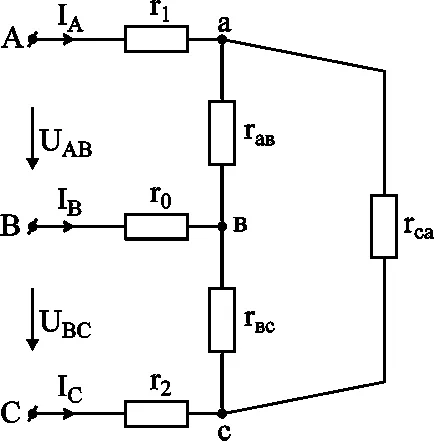
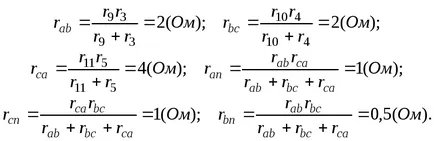
Получената трансформацията триъгълник в звезда (фиг. 3-10)
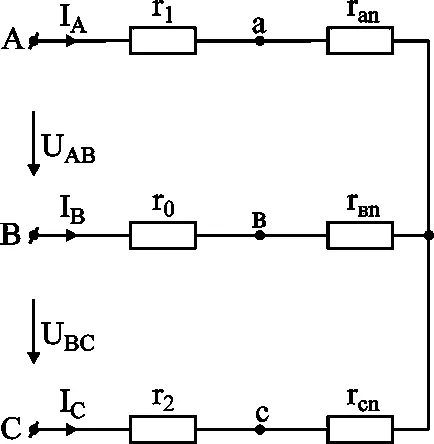
защото съпротивление R1; r0; R2 не са подложени на трансформация, през които тече ток желания IA; BC; IC. За да ги намерите, образуват система от уравнения на закон на Кирхоф:
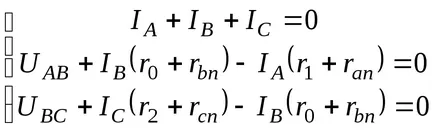
В резултат на решението, което се получи:
Превръщането на източник на напрежение с вътрешно съпротивление, източник еквивалентно ток с вътрешната проводяща обсъдено по-горе. Необходимостта да се замени един вид от друг източник, често се случва, когато решаване на проблемите. Трябва да се помни:
Равностойни източници разбират неизменност токове, напрежения и правомощия във външната електрическа верига, свързани с източниците.
Преобразуване активен триъгълника на активен звезда, и обратно, обсъдени по-долу.
схеми за преобразуване схеми.
схеми за преобразуване с два възела.
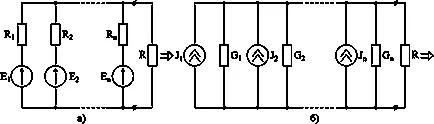
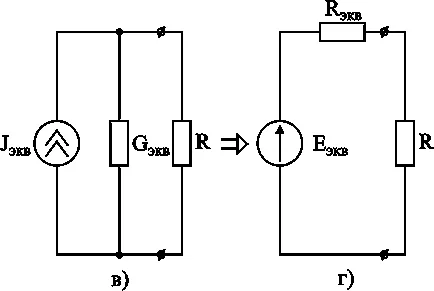
Ris.3-11. Превръщането на паралелни клонове връзка с източник на напрежение.
На ris.3-11 и електрическа схема е представена с две възлови точки, между които са свързани п успоредни клонове с EMF източници и резистор R. се изисква Тази схема за улесняване на един цикъл.
В първия етап (ris.3-11, б) прилагане на върховенството на еквивалентните източници на напрежение и ток.
Ако н източници на ток, свързани в паралел, източникът на еквивалентен ток:
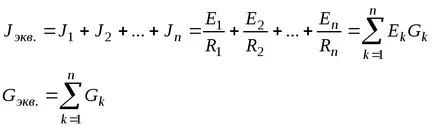
От диаграмата на фиг. 3-11, от своя страна, за да ris.3-11 схема, R, с помощта на отношенията:
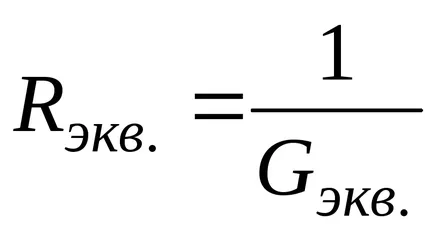
Формула (7) е понякога се нарича "формула за верига с два възела," или "Формула два възела."
Токът във външния контур (резистор R) е равен на:
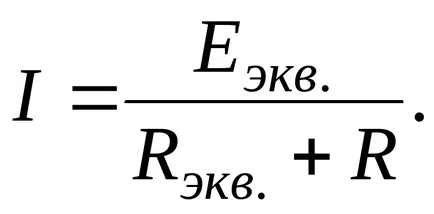
Прехвърляне на източници във веригата.
Изчислението е опростена в някои случаи и на електрическата верига, в резултат на прехвърляне на източници на ЕМП или ток.
От уравнения Кирхоф може да се види, че токът във веригата зависи от общия едн във веригите, а не от отделните компоненти. Ето защо, ако промените местоположението на източниците на ЕМП верига така че общата едн във всички вериги ще останат непроменени, това няма да се отрази на браншови течения.
По същия начин, напрежението на клонове определя от общия ток от всички източници на захранване. Ако промените местоположението на източниците на ток, така че общата сума на токовете в възли остават непроменени, то няма да повлияе на разпределението на стрес във веригата.
Условия прехвърлят източници на напрежение и източници на ток:
Ако искате да изключите източник на напрежение на клон, клонът е въведена в източник компенсиращо напрежение, и точно един и същ източник на напрежение се въвежда едновременно във всички отрасли, които се събират в определен бранш, възли.
И компенсиране на допълнителния източник на напрежение имат една и съща посока по отношение на разглеждания възел.
В резултат на това източник на напрежение на клона източник се изключва, а има и източници в другите отрасли. Комбинираните напреженията във всички вериги остават същите, съответно, не се променят браншови течения.
Заключение. източник на напрежение може да бъде преместен от клон верига във всички други клонове, свързани с възел на клона, без да се променя течения верига.
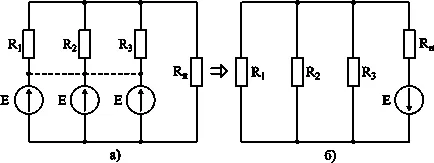
Фиг. 3-12. Прехвърляне EMF източници във веригата.
Така че, ако във всички отрасли, с изключение на една среща на възела, имат един и същ източник на напрежение (ris.3-12 както и), всички насочени към един възел или възел, а след това те могат да бъдат заменени с един единствен източник на напрежение в бранша в където източникът първоначално отсъства (ris.3-12 б).
Това е така, защото източника на напрежение клипове могат да се комбинират, за да означава равенство на съществуващия потенциал. В резултат на такава асоциация, показано на ris.3-12 и пунктираната линия схема се получава ris.3-12 б.
В случай, те прехвърлят източници на ток са свързани към верига възли, така че съвкупността остават постоянни токове на възлите.
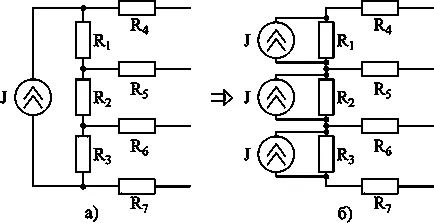
Ris.3-13. Преминаването на токовата верига източник.
На ris.3-13 и б настанят различни източници на енергия, но общият ток в двете схеми са едни и същи възли. Следователно, напрежението между възлите не се променя.
Заключение: източник на ток може да бъде заменен от източник на ток, свързан в паралелни разклонения, които се считат за схема с източник.
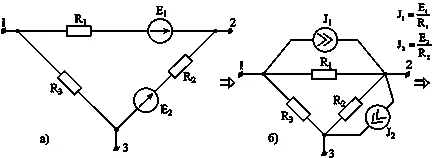
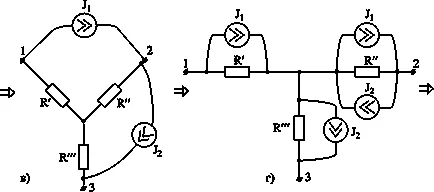
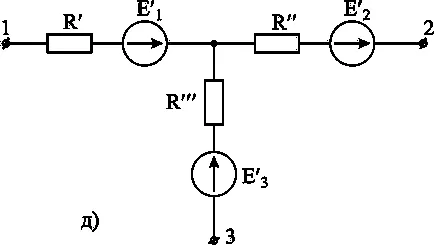
Преобразуване активен триъгълник в активна звезда и обратно.
Прехвърляне източници в Схема вярно в практиката комбинирани с различни методи за трансформация.
Следващите схеми илюстрират процедурата, дадена активна трансформация триъгълник към активното звезда.
Под активно триъгълника отнася до клонове верига са свързани делта и съдържа в допълнение към резистори източници на едн
Активно звезда се отнася до връзката на клонове в една звезда, чиито лъчи съдържат резистори и източници на ЕМП
Фиг. 4а показва част от веригата свързан делта, на които са включени клоновете източници едн