Вълшебната кутия - напречно сума разтвори примери магически кутии, магическите числа

Square - правоъгълник, в който всички страни са равни. И ако страните не са равни, а след това, счупване на правоъгълника в квадратни клетки, получаваме различен брой клетки в ред и колона. В този случай, не е възможно да се постигне еднакви суми за всички редове и колони едновременно. Отпуснете се на изискванията, ще се нарича магия правоъгълника, където сумата от номерата на всички линии са равни и отделна равно сумата от цифрите на всички колони, т.е. в правоъгълника ще бъде два магически суми, по един за редовете и един за колони.

Покана - обадете се, и може да го направим?

Нека да започнем с 2x3 правоъгълник (линии 2, 3 колона). Сумата от 1 + 2 + 3 + 4 + 5 + 6 = 21. дели на три, но не се дели на 2, което означава, че тези числа не могат да бъдат разпределени в два реда, така че сумата от номерата е същата.

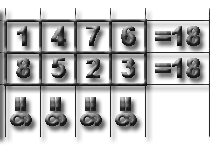
Ние продължаваме търсенето. 2x4 правоъгълник трябва да съдържа номера от 1 до 8. сумата от 1 + 2 +. + 8 = 36. и разделен на броя на редовете и броя на колоните. Чрез счупи цифрите по един чифт за същата сума, ние лесно се получи магията правоъгълник 2x4. Това е възможно да се направят първите изводи. Необходимо условие за неговото съществуване - сумата от цифрите да се организира, за да се раздели и броя на редовете и броя на колоните.

Освен това, съотношението на суми на линиите и относителните количества на стълбовете е равен на броя на колоните на шевове. Нека се обърнем към размера на 3x4. 5 = 1 +2+. + 12 = 78 не се дели на 4, ние лети без спиране на размера на 3x5. 1 + 2 +. + 15 = 120. неделими от 3 и 5, възможно правоъгълник.

Ние поставяме проблема по общ начин. Номера от 1 до NK необходими за пускане в правоъгълника на п редове и к колони, така че да образува две магически количество: S1 = (1 + NK) к / 2 за всяка линия и S2 = (L + NK) п / 2 за всяка колона след това на правоъгълника ще се нарича магически. Необходимо условие за изграждането на такъв правоъгълник намерени, доказа съществуването на два примера, продължи на една ръка разстояние.