В равнобедрен трапец са перпендикулярни диагонала

Ако диагоналите на равнобедрен трапец един са перпендикулярни, при решаването на проблема ще бъде полезен за следващия теоретичния материал.

1. Ако диагоналите на равнобедрен трапец един са перпендикулярни, височината на трапеца е равен на половината от сумата на базите.

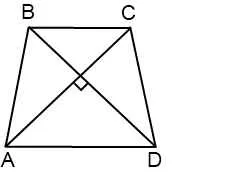
Чрез директен CF точка С успоредно BD, AD и ще се разшири до пресечната точка с линия CF.

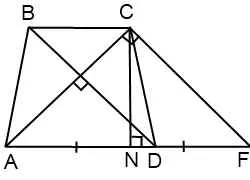
Четиристранни BCFD - успоредник (BC ∥ DF като основа на трапеца, BD ∥ CF според конструкцията). Следователно, CF = BD, DF = BC и AF = АД + BC.

ACF правоъгълен триъгълник (ако линията е перпендикулярна на една от две успоредни линии, перпендикулярна на нея, и от друга права линия). Тъй като в равнобедрен трапец диагонал са равни, и CF = BD, след CF = AC, т.е. ACF триъгълник - с AF равнобедрен база. Така че, това е и височината на медианата CN. И тъй като медианата на правоъгълен триъгълник, съставен към хипотенузата е равна на половината г.

което в общи линии може да се запише като

където H - височина на трапеца, а и б - неговата фондация.

2. Ако диагоналите на равнобедрен трапец един са перпендикулярни, височината му е равна на средната линия.

Тъй като средната линия на трапец М е равна на половината на основание, че

3. Ако диагоналите на равнобедрен трапец, перпендикулярна, областта на трапец е равна на квадрата на височината на трапеца (или половин сумата от квадратни основи, или на квадрата на разреза).

Тъй като районът на трапеца е дадено от

и височина, полу-сумата на основи и на средната линия на равностранен трапец с перпендикулярни диагонали са равни:

4. Ако диагонала на равнобедрен трапец са перпендикулярни, а след това на площада на своя диагонал е равен на половината от сумата на кв бази, както и два пъти квадрата на височината и два пъти квадрата на средната линия.

Тъй като изпъкнал четириъгълник площ може да се намери чрез диагонал, а ъгълът между тях съгласно формула

грях 90 º = 1, и диагоналите на равнобедрен трапеци са равни, тогава областта на равнобедрен трапец, чиито диагонали са взаимно перпендикулярни, равно