Universal уравнение на еластичната линия лъч

Да разгледаме Фигура 5.1. Лъчът на постоянно напречно сечение под влиянието на външен товар P се деформира, така че неговата крайна точка С се излъчва от позиция C1. Неутралната ос на лъча, наричан еластичен линия, в точката с координира Z е 1 / R кривина. ш деформация. ъгъл р = Y ¢. второ производно y².

Тези параметри са свързани с доказване в диференциална геометрия (5.1)

За малки премествания стойност у '2 в сравнение с 1 може да се пренебрегне, тогава: (5.2)

Като се има предвид (5.2) и (3.7.b), получаваме:

Като се вземат предвид отношенията (4.1) и (4.2) може да се получи верига на диференциални отношения в случай на лъч с променлива напречно сечение:

както и бар с постоянно напречно сечение:

По-специално, дървен материал за зареждане, постоянна част, равномерно разпределен товар Q:

Следователно, диаграмите в съответствие с диференциални уравнения (5.5), в зависимост от параметъра под внимание, ще имат следната форма (Фигура 5.2): Q - хоризонтална линия, Q - наклонена права линия М - квадратичен парабола, Q - кубичен парабола, у - кривата на четвъртия ред. Ако р = 0, но е концентрирана сила P. ос ще бъдат огънати от кривата на третия ред. Ако лъч е зареден само izkibayuschim момент М. изразена оста на кривата на втория ред.

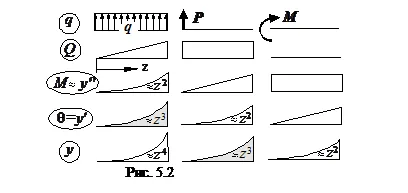
Най-голямото удължение и напрежението в пръчката се изчислява чрез формулите, получени от (4.6) и (4.7):

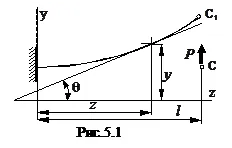
Определяне на деформация на гредата, показан на фигура 5.1. Огъващият момент в раздел Z е равно на: М = P (л - Z)

След двойно интегриране на изразяване

На интеграция константата С 1 е намерена от граничното условие: ако Z = 0imeem: у ¢ = 0. Следователно С1 = 0, но общият разтвори още напусне този термин във формулата:

На интеграция константата С 2 се определя от границата условие: Z = 0, когато у = 0. Съответно, С2 = 0, тогава за произволна точка:

Максималният ъгъл на наклона и деформацията се извършва в точката на прилагане на сила F.

Така, Z = л имаме:

Universal уравнение на еластичната линия лъч

От Пример 5.1 показва, че има две произволни константи (C1, C2 5.9) за всяка част лъч след интегриране уравнение. Ако гредата има п сайтове, за да се определи 2n интеграция константи трябва да работят заедно за решаване на 2n уравнения. За излъчване на постоянна скованост EJx това може да се избегне при подготовката на еластичната линия на уравнението да се следват определени правила.

Разглеждане на лъча (фигура 5.3), натоварени с най-често срещаните видове напрежения: концентрира момент Ма. точка сила Р и интензивност разпределен товар р. От тези видове силови фактори може да се комбинира с почти всички възникващи в практиката, видове товари. За положителните посоки на силите, които се движат от левия край ще вземе тези, посочени във фигура, т.е. Р и Q - до, и за миг Ма - по часовниковата стрелка. определен фактор енергийна система трябва да отговарят на условията за равновесие.

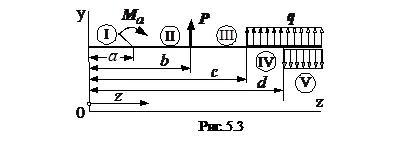
Разкриват функции, въведени в уравнението на еластичната линия различните видове външни сили. За да направите това, уверете израз на огъващи моменти за всеки един от петте области, посочени по-долу:

Вижда се, че огъващият момент за всяка следваща точка изцяло включва експресия на огъване момента на предишния раздел и то е различно от добавянето на новия план. В прехода от четвъртата част на споменатия пети модел съхранява специално. Така равномерно разпределен товар на четвъртата секция продължава, както е показано с пунктир на петия част и петата част едновременно прилага отрицателен (компенсиране) интензитета на р натоварване.

Ние интегрираме полученото израз веднъж, без да разкрива скобите. За да се поддържа еднаквост на получените изрази, интеграл на запис Vi Vi (Z-а), което ще се отрази само величината на произволен постоянен Ci. В резултат, като се вземе предвид експресията y² = M / EJx получи следния израз за ъгъл у еластичната линия ":

Произволни константи Ci. Те трябва да бъдат избрани така, че преминаването от една секция в друга стойност у "не претърпя разкъсване. Следователно, с Z = и u'1 = Y2, ако Z = В = u'3 J2, и така нататък.

Тъй като лъч има постоянна скованост, очевидно е, че

Ъгълът на наклона q0 еластичен линията в основата се определя от експресията на първата част:

Интегриране на изразите, получени за втори път ще намерите:

Произволни константи Ди Тя трябва да се избира от състоянието на непрекъснатост на у функция на границата. Следователно, с Z = Y1 и Y2 =, ако Z = В = Y 2 Y 3 и т.н. Тъй като лъч има постоянна скованост, очевидно е, че

,

където y0 - координира еластична линия на произхода. Уравнение (5.14) е удобно написана под формата на обща, така наречената еластична лъч линия на универсалната уравнението. (5.15)

За определяне на координатите на точки на еластичната линия на първата част трябва да се използва от членовете на уравнението вляво от вертикалната линия с индекс I. За втората част необходимо да се заемат с условията индексни функции II. и т.н. За определяне на ординатата на петото станция трябва да се калкулира, като се използва цялото уравнение 5.15. Предимството на универсалната уравнение е, че тя ви позволява да направите уравнението на еластичната линия, заобикаляйки тромава определението на произволни константи. Независимо от броя на обектите, е необходимо да се определи само две константи: v0 и q0.

Добави уравнението на еластичния линия на конзолата с левия край неподвижно захванат и се зарежда в средната част на разпределен товар Q (Фигура 5.4). Определяне на реакцията и момента, в запечатване на:

Сега е възможно, вместо на левия печат в схема еквивалент направи го поддържа реакция. По този начин, схемата намалява до формата, за които е изписано универсално уравнение. Произходът е поставен в левия край на гредата. Тук q0 = 0 и y0 = 0.

Освен това, от уравнението (5.15) "наемат" на уравнението условията, съответстващи на разглеждания лъч.

Първата част включва силата условия и въртящ момент в zadelke. Във втората част се добавя към тях терминът разпределен товар. Третата част на изместването е определено всички условия на уравнението. Ако отворите на скобите, след последната част получаваме:

.

Тук еластичната линия е права линия, тъй като огъващият момент е нула.