Свързване на графиката - studopediya

Ненасочена графика се нарича връзка. ако всяка двойка различни върхове могат да бъдат свързани с най-малко една верига.

А насочено графика се нарича силно свързани. Ако по някаква два върха XI и XJ да има най-малко един път, свързващ XI към XJ.

А насочено графика се нарича еднопосочен свързан. ако поне един е достъпен от друга страна, за каквито и да било два върха.

Свързаните компоненти на ненасочена графика се нарича свързан подграф, а подграф не е собственост на друг свързан подграф на графиката (най-свързания подграф).

Компонент на насочена графика силно свързана се нарича силно свързан подграф не е собственост на друг подграф силно свързан подграф на графиката (най-силно свързан подграф).

, Единичен компонент за свързване на ненасочена графика е неговата едностранно свързан подграф не е собственост на друг подграф едностранно свързан подграф на графиката (максимум едностранно свързан подграф).

Нека G = (X, А) ненасочена графика-TION с множество върхове X = x1. хп>. Квадратна матрица S = (Сий) на за п, в която

G се нарича матрицата на графиката.

За насочено графика квадратна матрица Т = (tij) на за п. от кото-много

nazyvaetsyamatritsey едностранно връзка (достъпност).

Квадратна матрица S = (Сий) на за п. в която

Тя се нарича матрица на силна връзка.

В ненасочена графика, показана на Фиг. 3.8 Двете свързаните компоненти. Първият компонент включва връх свързаност x1. x2, x4, x5, а вторият се състои от един връх x3.

свързаността на матрицата на графика има формата:

Виждаме, че 1-во, 2-ро, 4-то и 5-то редовете на матрицата S са идентични.

В насочено графика, показана на Фиг. 3.9 Двете компоненти на силна свързаност. Първият компонент включва връх свързаност x1. x2, x3, х5, а вторият се състои от един връх x4. Всъщност, за всеки чифт върхове от набор x1. x2, x3, х5> има най-малко един път на свързването на тези върхове. Така например, на пътя (x1. X2, х5, x3, x1) свързва всички тези върхове. От върха на x4 няма начин всеки един връх на графиката.

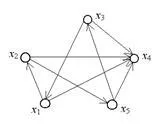
Matrix силна свързаност на графиката се изчислява по формулата:

Ние виждаме, че 1-ви, 2-ри, 3-ти и 5-ти редовете на матрицата S са идентични.