Състоянието на равновесие на телата

баланс на тялото се нарича състояние, в което всяко ускорение на едно тяло е равна на нула, тоест всички действия на силите на тялото и моменти са балансирани сили. В същото време тялото може да:

да бъде в състояние на покой;
равномерно движение по права линия;
равномерно се върти около ос, която преминава през центъра на тежестта.

равновесни условия тяло

Ако тялото е в равновесие, са едновременно изпълнени двете условия.

Сумата на вектор на всички сили, действащи върху тялото е равна на нула вектор: $ \ sum_n> _n> = \ overrightarrow $
Алгебричната сума на всички моменти на силите, които действат на едно тяло е равна на нула: $ \ sum_n = 0 $

Необходими са две равновесни условия, но не са достатъчни. Ето един пример. Помислете равномерно въртене на колелата, без подхлъзване върху хоризонтална повърхност. са изпълнени двете равновесни условия, обаче, тялото се движи.

Да разгледаме случая, когато тялото не се върти. За да се гарантира, че тялото не се върти и е в равновесие, е необходимо, че сумата от проекциите на всички сили върху произволна ос е равен на нула, т.е. резултантната сила. Тогава тялото и в спокойствие, или се движи равномерно в права линия.

Тялото, което има една ос на въртене, ще бъде в равновесие, ако следното правило въртящи моменти: Сумата от моментите на силите, които се въртят по часовниковата стрелка на тялото, трябва да са равни на сумата от моментите на силите, които се въртят в обратна на часовниковата стрелка посока.

За да се получи точното време с най-малко усилия, силата, да се упражнява сила, доколкото е възможно, от оста на въртене, което води до повишаване на ръката момент и намаляване на стойността на силата, съответно. Примери на органи, които имат ос на въртене. лост, блокове за врати, бормашина и така нататък.

Три типа равновесие на телата, които имат опора

стабилно равновесие, ако тялото се извлича от позицията на равновесие в близко съседна позиция и оставят на мира, за да се върнете на тази позиция;
неустойчиво равновесие, когато тялото се извлича от равновесното положение в съседна позиция и оставят на мира, ще има повече, за да се отклони от тази позиция;
безразличен равновесие - когато тялото е получен в съседна позиция и оставят на мира, ще остане в новата си длъжност.

тяло равновесие с фиксирана ос на въртене

устойчиви, ако равновесното положение на центъра на тежестта заема най-ниската позиция на всички възможни разпоредби съседите и нейната потенциална енергия ще има най-ниската стойност на всички възможни стойности в съседни позиции;
нестабилна, ако центърът на тежестта е на най-високата от всички съседи на разпоредбите, както и потенциалната енергия е с максимална стойност;
безразличен, ако центъра C на тежестта на тялото във всички възможни позиции на съседите на същото ниво, както и потенциалната енергия в тялото на прехода не се променя.

На телесна маса М = 8 кг доставени върху грапава повърхност на хоризонталния участък. За тяло свързана нишка изхвърля през блок В (фигура 1 а). Що за F може да връзвам на края на конеца, е спряно от блока, така че да не се наруши равновесието на тялото на? Коефициентът на триене е = 0,4; пренебрежимо триене блок.

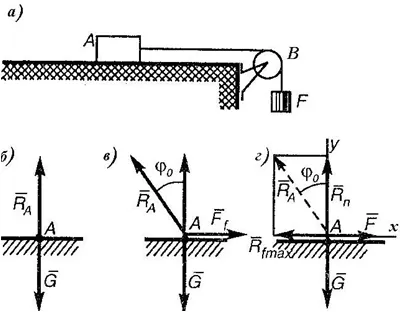
Ние дефинираме теглото на тялото

G = мг = 8 $ \ cdot $ 9,81 = 78,5 N.

Ние вярваме, че всички сили се прилагат към тялото А. Когато тялото е поставен върху равна повърхност, след това действат върху него само две сили: (. Фигура 1, б) тежестта G и обратна посока подкрепа RA отговор.

Ако проявяват някои сила F, действащи по протежение на хоризонтална повърхност, отговорът RA, балансиране на силите G и F, започва да се отклонява от вертикалата, но тяло ще бъде в равновесие, докато модул сила F не надвишава максималната мощност Rf макс триенето съответстващо на граничната стойност на ъгъл $$ о (фиг. 1с).

Разширяване на отговор RA за двата компонента Rf макс и Rn, ние получаваме система от четири сили, приложени към същата точка (Фиг. 1d). Проектиране тази система на сили на х и у ос, ние получаваме две уравнения на равновесие:

Ние решаване получената система от уравнения: F = Rf Стах, но Rf = макс е $ \ cdot $ Rn и Rn = G, така F = F $ \ cdot $ G = 0,4 $ \ cdot $ 78,5 = 31,4 Н; m = F / г = 31,4 / 9,81 = 3,2 кг.

А: Тегло на натоварване т = 3,2 кг