Списък ( "маса") основни интеграли

Ние списък интегралите на елементарни функции, които понякога са наричани маса:

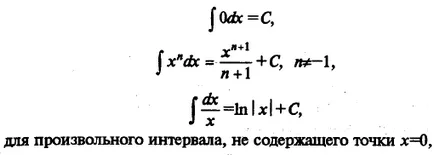
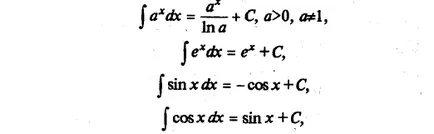
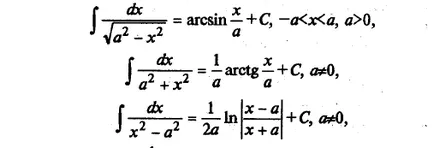
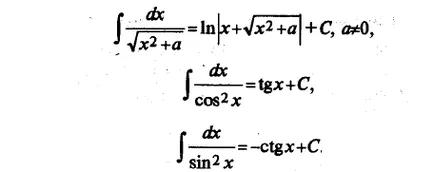
Всеки от горните формули може да се докаже, като производното на дясната ръка (като резултат от функцията подинтегрален се получава).

методи за интеграция

Нека разгледаме някои от основните методи за интеграция. Те включват:

1. Метод разлагане (директно интегриране).

Този метод се основава на директно използване на таблични интеграли и на свойствата на приложения 4 и 5 от неопределен интеграл (т.е. за отстраняване на скоби постоянен фактор и / или представянето на подинтегрален като сума от функции на - разлагане на подинтегрален по отношение).

Пример 1. Например, за nahozhdeniya (DX / х 4) може директно да се използва табличен неразделна dlyax п DX на. В действителност,  (DX / х 4) = x -4 DX = х -3 / (- 3) + С = -1 / 3 х 3 + C.

Разполагате с няколко примера.

Пример 2. В същия nahozhdeniyavospolzuemsya интеграл:

Пример 3. За да nahozhdeniyanado

Пример 4: За да откриете, ние представляват подинтегрален в videi употреба табличен интеграл за експоненциална функция:

Обмислете използването на отстраняването на скоби постоянен фактор.

Пример 5.Naydem пример. Имайки предвид, че. получаваме

Пример 6 Да. Тъй като ние използваме табличен integralomPoluchim

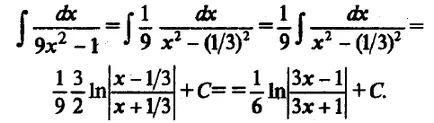
Следните два примера може да се използва за отстраняване на скоби и таблични интеграли:

Нека разгледаме по-сложни примери, в които на интеграл от количеството използвани.

Пример 9. Например, ние откриваме

. За да се прилага метода на разлагане в числителя на формулата за размера на използване на  куба. и след това получената полином е разделена от срока на знаменател от план.

=  ((8x 3/2 + 12x + 6x 1/2 + 1) / (х 3/2)) DX =  (8 + 12x -1/2 + 6 / х + х -3/2) DX = 8 dx + 12x -1/2 DX + + 6dx / х + x -3/2 DX =

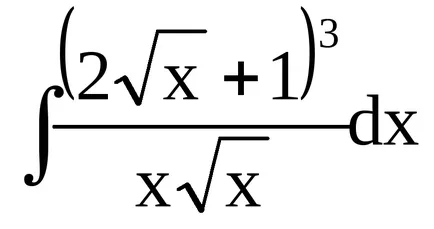
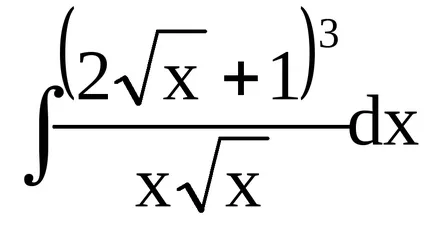
Трябва да се отбележи, че в края на един записани решения обща константа C (а не индивидуално чрез интегриране на всеки термин). В бъдеще също предложи да пропуснете процеса на интегриране на устойчиви решения за конкретните условия, докато изразът съдържа поне един неопределен интеграл (ще пиша постоянно решение в края на краищата).

10. Пример Нека. За да се реши този проблем, за да фактор числител (тогава да бъде в състояние да намали знаменател).

11. Пример Нека. Можете да използвате тригонометричните идентичност.

Понякога, за да се разложи изразът в условия, е необходимо да се използват по-сложни техники.

12. Пример Нека. В подинтегрален ние подбираме цялата част от фракцията. след това

.

13. Пример Нека

2. Метод замяна променлива (метод заместване)

Методът се основава на следната формула: f (х) DX = f ( (т)) ` (т) DT, където х =  (т) - функция, която е диференцируема в разглеждания интервал.

Доказателство. Ние считаме, производни променлива TGI наляво и надясно части на формулата.

Имайте предвид, че от лявата страна е сложна функция, което е междинно съединение аргумент х =  (т). Следователно, за да се диференцират го спазва към Т, е диференцируема първата съставна над х, след това vozmem производно на междинно съединение аргумент отношение на тон.

Производното на дясната ръка:

Тъй като тези производни, че за разследването на теоремата на Лагранж лявата и дясната страна се оказаха формули се различават с константа. Тъй като неопределени интеграли самите са определени до неопределен постоянен срок, за определена константа може да бъде намалена в крайния запис. Той се оказа.

Успешна смяна на променливи, за да се опрости оригиналния интеграл, а в най-простите случаи, за да се сведе до масата. При прилагането на този метод се разграничат методи за линейни и нелинейни смяна.

а) метод линеен заместване от примера.

Пример 1.

. Pustt = 1 - 2х, след това

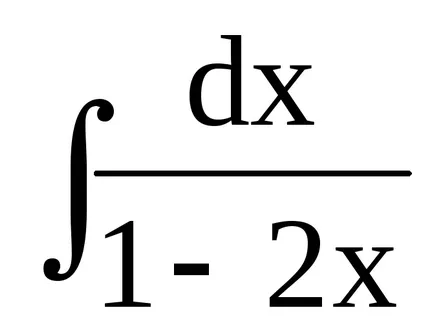
Трябва да се отбележи, че една нова променлива, не можете да пишете на кирилица. В такива случаи ние казваме за функцията за конвертиране на диференциално марка или въвеждането на фиксирани и променливи диференциал марка - т.е. имплицитната промяна на променлива.

Пример 2. Например, naydemcos (3x + 2) DX. Чрез диференциална свойства DX = (1/3) г (3 х) = (1/3) г (3x + 2), togdacos (3x + 2) DX =  (1/3) COS (3x + 2) г (3x + + 2) = (1/3) cos (3x + 2) г (3x + 2) = (1/3) грях (3x + 2) + С

И в двата примера линейната пермутация Т = KX + б (k0) се използва за намиране на интегралите.

Като цяло, следната теорема притежава.

Теорема за линейна смяна. Нека F (х) - примитивна за F функция (х). Togdaf (KX + б) DX = (1 / к) F (KX + б) + C, където к и б - са константи, k0.

По дефиниция f неразделна (KX + б) б (KX + б) = F (KX + б) + С Ход (KX + б) = (KX + б) `DX = kdx. Топено постоянна mnozhitelkza неразделна знак: kf (KX + б) DX = F (KX + б) + С Сега е възможно да се разделят на лявата и дясната страна на уравнението, за да получите точна твърдение Naki да се позова на постоянен мандат.

Тази теорема гласи, че ако определянето на неразделна f (х) DX = F (х) + C, вместо експресия аргумент х заместител (KX + б), това ще доведе до допълнителен фактор 1 / kpered примитивни.

Следващите примери ще решат Използвайки горната теорема.

Намерени. Zdeskx + б = 3 -x, t.e.k = -1, б = 3. След

Намерени. Zdeskx + б = 4х + 3, t.e.k = 4, б = 3. След

Намерени. Zdeskx + б = -2x + 7 t.e.k = -2, б = 7. След

.

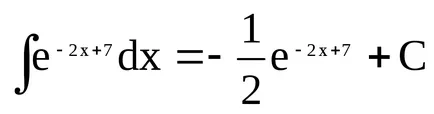
Пример 6 Нека

. Zdeskx + б = 2х + 0 t.e.k = 2, б = 0.

.

Сравнете този резултат с пример 8, която се разделя чрез разлагане. Решаването на този проблем е друг метод, имаме отговора

. Ние сравняваме резултатите. По този начин, тези изрази се различават с константа, т.е. отговорите не са в конфликт помежду си.

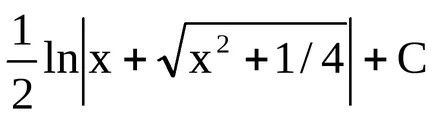
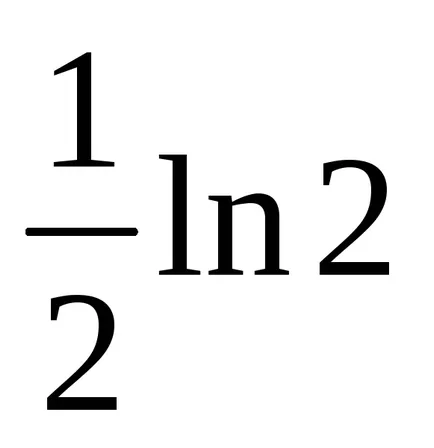
Пример 7. Ние намираме

. Различаваме в знаменателя на точен квадрат.

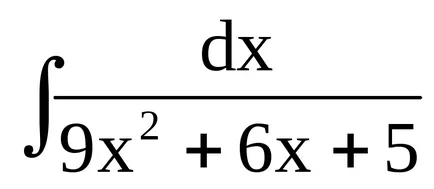
В някои случаи, подмяна на променливата не намалява интеграл директно на масата, но може да опрости решение, което дава възможност да се използва в следващ етап на метода на разлагане.

Пример 8 Например намери. Zamenimt = х + 2, togdadt = г (х + 2) = DX. след това

,

където С = С1 - 6 (когато заместен vmestotvyrazheniya (х + 2), вместо на първите две условия ½x получаване на 2 -2x- 6).

Пример 9. Откриване

. Pustt = 2х + 1, togdadt = 2dx; DX = ½dt х = (t-1) / 2.

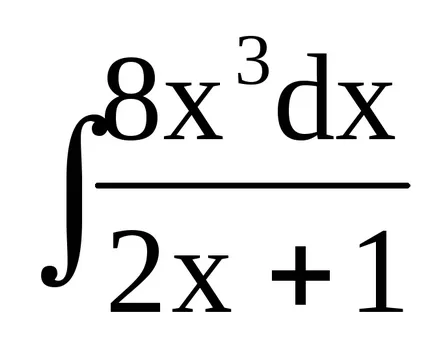
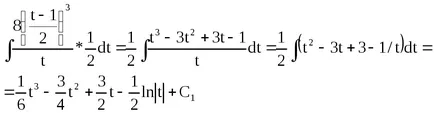
Ние заместват tvyrazhenie (2х + 1), и показват скоби дават подобни.

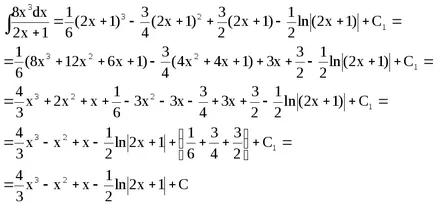
Имайте предвид, че в процеса на промяна, ние се движим към различен постоянен срок, тъй като Група постоянни условия в процеса на трансформация могат да бъдат пропуснати.

б) метод нелинейна заместване, разгледаме следния пример.

Пример 1.

. Pustt = -x 2. След това може да се изрази х cherezt, след това се намери израз за DXI реализира промяна на променливата в желания интеграл. Но в този случай е по-лесно да се направи по друг начин. Naydemdt = г (Х2) = -2xdx. Имайте предвид, че vyrazheniexdxyavlyaetsya фактор на подинтегрален в тази интегрална. Ние го експресират от получения ravenstvaxdx = - ½dt. след това

=  (- Уг) д т DT = (- Уг)  д т DT = (- Уг) д т + C = (- Уг)+ C

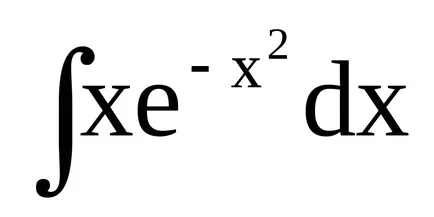
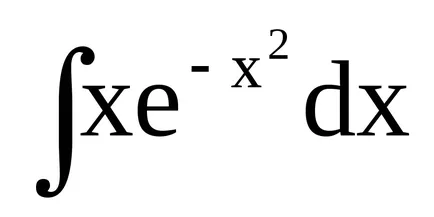
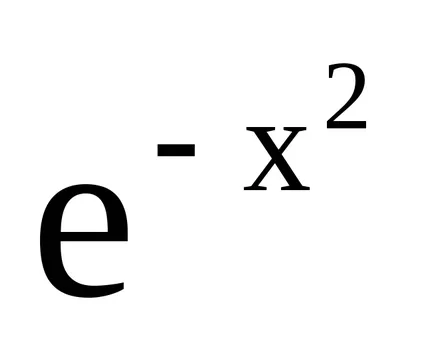
Разполагате с няколко примера.

Пример 2. Find. Pustt = 1 -x 2. След

;

Пример 3: Да. Pustt =. след това

;

Пример 4. В случая на не-линейна заместване също е удобно да се използва имплицитно промяна на променливата.

Например, ние откриваме

. Zapishemxdx = = (-1/4) г (3 - 2x 2) (имплицитно заменя peremennoyt = 3 - 2x 2). след това

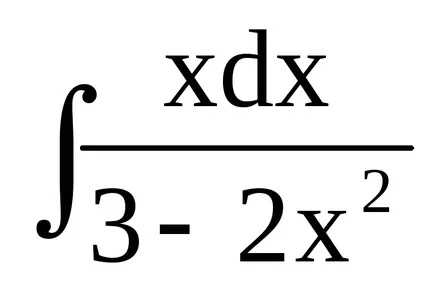
Пример 5 Нека. Тук също се въведе променливо диференциално марки (имплицитно zamenat 3 + 5x = 3). след това

Пример 6 Да. защото,

.

Пример 7. Да. Оттогава

Помислете за няколко примера, в които има нужда да се съчетаят различните заместване.

Пример 8. намерен. Pustt = 2х + 1, togdax = (t-1) / 2; DX = ½dt.

Пример 9. намерен. Pustt = х- 2 togdax = т + 2; DX = DT.