Скоростта на функция промяна

Начало | За нас | обратна връзка

Определяне на функцията производно чрез граница

Да предположим, че в квартал на функцията е определена в функцията производно е граничната точка, ако има такъв,

Конвенционални определяне на функцията производно в точка

Производното на функцията на точка. е границата, не може да съществува или съществува и да бъде ограничен или безкрайно. Функцията е диференцируема в точка, ако и само ако неговото производно в този момент съществува и е ограничен:

За диференцируеми функции в района на справедливо представителство

Забележки Наричаме нарастване на аргумента, а стойността на нарастване на функцията в точката на време

· Нека функцията е с краен производно на всеки момент от време функцията производно

· Функция, която е производно в точка, е непрекъсната. Обратното не винаги е вярно.

· Ако самата функция производно е непрекъсната, а след това на функцията се нарича непрекъснато диференцируема и записване:

Геометрична и физически смисъл на производното

Наклонът на допирателната

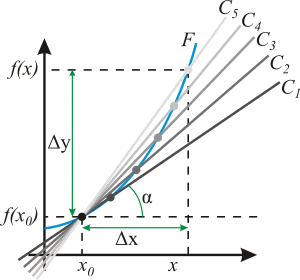
Геометрична смисъл на производно. В графиката на x0 е избран абсцисата и ординатата, съответстващ на изчислената F (x0). В tochkix0 в близост избран произволна точка х. Чрез съответния напречното (първата С5 светлосив линия) в графиката на функцията F се провежда точка. разстояние # 916 х = х - x0 клони към нула, в резултат на пресичане преминава допирателна (постепенно потъмнява линия С5 - С1). На допирателната на ъгъла # 945; наклона на допирателната - е производно на точка x0 на.

Ако функцията има ограничен производно в точка в близост може да се изчисли приблизително чрез линейна функция

Функцията се нарича допирателната към броя на точка е наклон или допирателната на ъгъл naklonakasatelnoy линия.

Скоростта на функция промяна

Да - закона за праволинейно движение. След това тя изразява моментната скорост на движение по време на втората производна изразява мигновено ускорение на време

Като цяло, производно на мястото изразява степента на промяна на функцията на. т.е. скоростта на потока на процеса, описан в зависимост

Производни на по-висок ред

Концепцията на производно на всеки ред се определя рекурсивно. Ние вярваме,

Ако диференцируема функция. първата производна цел е дадено от

Да предположим сега, че производното на ред се определя в близост до точката и диференцируема. след това

Ако функцията е в определени граници D на частна производна на една от променливите, наречен производно, се функция на това може да има някакъв момент частични производни за еднакви или за всяка друга променлива. За първоначалната функция на тези производни са частични производни от втори ред (или втората частична производни).

Частичното производно на втория ред или по-висока, взети от различни променливи се нарича смесена частна производна. Например,

Операцията за намиране на производното се нарича диференциация. По време на тази операция, често работи с частни, сума, характеристиките на продукта, както и с "функции на функции", която е сложни функции. Въз основа на определението за дериватив, то е възможно да се установи правилата на диференциация, за да се улесни тази работа. Ако C - постоянна и е = е (х), G = грам (х) - някои диференцируеми функции, тогава следните правила на диференциация:

• Ако функцията е дадена по параметри:

· Формула производни на и отношения могат да се обобщят в случай на диференциация на п-кратно (Лайбниц формула):

където - Биномен коефициент.