Системни сравнения, сравнения на първа степен на системата - метода на теория сравнение

Системни сравнения от първа степен

Системни сравнения на първа степен със същия неизвестен, но с различни модули, написани в общ вид, както следва:

Общ метод (Метод последователни разтвори) е, че първата е на първо сравнение, при което - числата малката неотрицателни или абсолютно малката остатъчни модул и beretsyaklass

удоволствие, отколкото първия.

След това тази стойност е заместен във втория сравнение chtodaet

където отново в един клас от числа е заместен в уравнението (.

В резултат се получава стойност в техния клас, които отговарят на първите две сравнения система. След това тази стойност е заместена в трета сравнението на системата, както и след това е заместен в четвърта система сравнение и т.н.

Имайте предвид, че е възможно да се отиде в малко по-различен начин: на първо място, всеки на системата се постига сравнения и е представен като:

и след това се получава по начина, описан.

Ако се окаже, че най-малко едно от сравненията на системата (4.1) няма решение, или сравнение по отношение на описания метод не може да бъде решен, тогава системата (4.1) няма разтвор.

Ако системата на Сравнения (4.1) и режещ елемент и модула на всеки сравнение, ние получаваме системата:

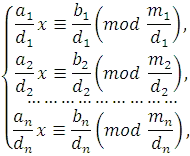
Сравненията на тази система могат да бъдат решени за намаляване и разтворът на система (4.3) към разтвора:

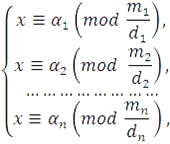
Ако системата (4.2) модулите по двойки прост, разтворът е възможно да се намери не obschimsposobom по-горе, и съгласно формулата:

където има решения на сравнения:

Разтворът на системата е:

Този метод може да се реши системата (4.4), ако модулите са взаимно прости.

Пример 1: решаване на системата за сравнение:

класове остатък. ако имаме:

1). следователно, той отговаря първата система сравнение,

2). Ето защо, той отговаря на втората система сравнение.

Следователно, клас остатък е разтвор. Можете да запишете на класа по различен начин: чрез добавяне към устройството 9, ние откриваме, че

Така че, тази система има сравнения разтвор