символична регресия
От машинно обучение.
Символичен регресия - метод за изграждане регресионни модели, като се опитва различни произволни суперпозиции на функциите на даден набор. Състав на функции в същото време се нарича "програма", и стохастични оптимизационни алгоритми за изграждане на такова наслагване се нарича генетично програмиране.
Изявление на проблема
Проблемът за намиране на оптимален модел за регресия структурата на повече свободни променливи следва. Комплект за вземане на проби - много _1, \ ldots \ mathbf_N | \ mathbf \ в \ R ^ М \> "> стойности на свободните променливи и много от съответните зависими променливи стойности обозначи тези двете групи като наборът от входни данни ..
Също даден набор от "> гладки параметрични функции, \ cdot \ cdot \ ldots \ cdot)" >. Първият аргумент на функцията - параметрите на вектор-ред "> последващо -.. Променливи от множеството на реалните числа, се разглеждат като елементи на вектора на свободните променливи Помислете суперпозиция, състояща се от не повече от функциите Това суперпозиция определя параметричен модел регресия, \ mathbf)" / >. Моделът на регресия в зависимост от вектора на свободните променливи "> и вектора параметри" >. Вектор \ в \ ^ R W "> се състои от свързани вектори функционални параметри, т.е., = \ mathbf_1 \ vdots \ mathbf_2 \ vdots \ ldots \ vdots \ mathbf_r" >, където - знак вектори присъединяване. Означаваме "> - набор от суперпозиции, индуктивно, генерирани от набора.
Вие трябва да изберете модел, който осигурява максимума, определен функционален | D) ". > Този функционален определя целевата функция)" >, който се използва при изчисленията.
Процедурата за търсене на оптимален модел
Търсене оптимален модел се предлага в разнообразие от модели, генерирани на всяка итерация на алгоритъма. Преди операцията на алгоритъма даден набор от измерените данни и набор от гладки функции. Задайте начален набор от конкурентни модели, където всеки модел е суперпозиция на функциите \> _ ^ ">. Ако няма първоначален набор от модели, тя се генерира на случаен принцип. Освен това, последователността на стъпките по-долу.
1. Метод за конюгат градиент (или други настройки метод) са сведени до минимум наказателни функции) "> за всеки модел. Опции са намерени ^ \ m_i" > и изчислената стойност на наказание функцията на всеки модел.
2. Задайте следните правила за конструиране на модели на деривати. Всеки модел е конструиран производно модел. В произволно избрана функция ">. Изберете един модел на" > и произволна функция ">. Моделът е генерирана от функцията за модел чрез замяна" > с аргументи си към функцията "> със своите аргументи.
3. предварително определена вероятност модел на всеки подлага на промяна. Променливата модел -taya избрана функция, както и правото на вероятностно разпределение набор избор на функция. От множество произволно избрана функция, и замества функцията. Hyperparameters "> Тази функция се определя като)" >. Vector параметрите на тази функция _ "> е равен на нула или възложени със задачата.
4. При избора на модел на единен набор от майки и деца модели в съответствие с критерия) ">, за да изберете най-доброто, за да се използва в следващите повторения.
Алгоритъмът се спира, когато грешката не надвишава предварително определена или когато определен брой пъти.
Един пример за модел на сграда
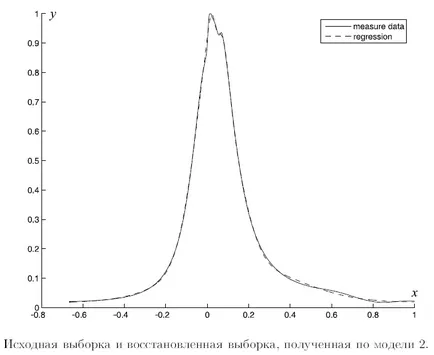
Следното описва пример за изграждането на символна регресионен модел. Фигура 1. Твърдият крива показва необработените данни, пунктираната линия показва стойностите на регресионния модел. Абсцисата на стойността на един свободен променлива, и ординатната ос - стойността на зависимата променлива. Пробата, представено с тази крива се състои от четири хиляди проби. Експертите са дадени набор от основни функции на елемента, от които се генерират от регресионния модел. Списъкът на функциите е дадено в таблицата. Много от първоначалния модел на сближаване също бе дадена от експерти.

Изборът на модели, произведени от повече от хиляда генерирани модели. Таблица 2 показва трите модела получени чрез алгоритъма. Качеството на образците се определя чрез грешки и броят на параметрите в вектор параметър "> Грешка -. RMS относителна грешка
грешка - максималната относителна грешка

линия "описание" таблица на 2 показва структурата на модела на дърво. Като пример, че моделът 2. Моделът се състои от суперпозиция от осем функции. Функции и събиране и умножение са първи аргумент празни параметри вектор; И _4 \ cdot) ">. Функции \ sigma_i> \ MBOX \ наляво (> \ вдясно)" > са параметрите на векторите _I = \ langle \ lambda_i \ mu_i \ sigma_i, "> и функция Той има параметър вектор _4 = \ langle.
Моделът може да бъде пренаписана като \ х) = L (\ mathbf_4, х) ^ \ пъти \ наляво (х + \ sum_³h (\ mathbf_i "> където = \ mathbf_1 \ vdots \ mathbf_2 \ vdots \ mathbf_3 \ vdots \ mathbf_4 "> Блог преглед на моделите .: