Сегмент, който свързва центъра на кръга с всяка точка на едно и също - представяне 15733-4

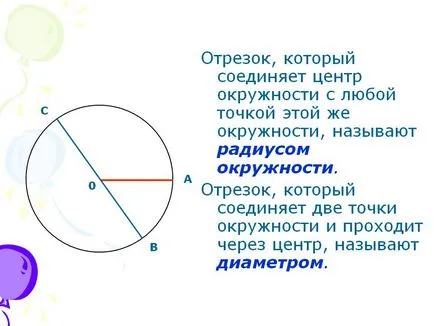
Сегмент, който свързва центъра на кръга с всяка точка на кръга, се нарича радиуса на кръга. Сегмент, който свързва две точки на окръжността и минава през центъра, наречен диаметъра.

Слайд 4 на представянето "на кръга, а на кръга" на урок по геометрия на "The Circle"

Размер: 960 х 720 пиксела, на формат: JPG. За да изтеглите слайда, за да бъде използвано на урок геометрия, щракнете с дясното изображение бутон на мишката и натиснете бутона "Съхраняване изображението като. ". Изтеглете цялата презентация на "Кръгът и krug.ppt" може да бъде в цип архив размер на 231 KB на.

кръг

"Вписана окръжност" - вписан кръг. Предвид: AB, AC - тангенти, B, C точки на допиране ъгъл BAC = 56 °, OS = 4 cm Saynakova Расим Sayfullovna математика учител ноември Zyryanskaya SOSH № 2. търсене: ъгъл CCA RH .. Докаже: О точката на пресичане на ъглополовящи на ABC ?. Теорема: кръг, може да се впише във всеки триъгълник. EFMN окръжност около кръг описано DKMN не е около кръг.

"Допирателната към окръжност» - допирателна М. собственост. Точката за докосване. Знак на допирателната. Нека г - разстояние от центъра O към линията КМ. О. сегменти AK и СЪМ сегмента, наречени тангенти, извлечени от А. След това. Tangent.

"The окръжност кръг" - който е на еднакво разстояние от центъра на триъгълник вписан в окръжност? Центристи. Polygon - вписан. Това, което е описано от един кръг? Вписан многоъгълник. Триъгълници и кръгове. Какво е дъга? Триъгълниците Как възникна идеята за един кръг? Как се пише \ описваме кръг на щастието?

"Ellipse" - Какво е елипса. Кратери на Луната също имат елипсовидна форма. Ellipse. Нека да се движи молива върху хартията, така че конецът остава опъната. Оказва се, че всички планети се движат около Слънцето не е кръг, но елипса. Закрепете краищата на конеца трикове. Общата точка се нарича точката на контакт. Tangent.

Само на "Кръг" тема 21 Представяне