Седем начина да намерите областта на триъгълник

И така, днес, ние считаме този забележителен геометрична форма, като триъгълник. Повече подробности за намирането на площта на триъгълник.

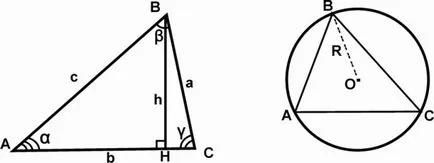
Имам определени седем основни начини за намиране на площта на триъгълника. Нека ги разгледаме по-подробно.

1. Ако ни се дава всяка страна на триъгълника, а надморската височина привлечени към тази страна, тогава ние просто заместване на тези стойности във формулата.
2. Ако имаме дължината на двете страни на триъгълник, а ъгълът между тях, а след това ние използваме формулата.
3. И ако дадена задача и на трите страни на триъгълника. е да се намери на площ имаме нужда от формула на Херон. където - semiperimeter.
4. Има такова формула, която, свързани с областта на триъгълник, където радиусите на вписаните окръжности и фигурата. Но основните от тях ние не се интересуват, защото трябва да има три страни на триъгълника, и ако те са, а след това площта на триъгълника могат да се намерят формула херона, тогава ние не се нуждаят от радиуса (те се използват в случаите, когато това е необходимо, за да намерите най-радиус okruznosti ). Но ако имаме само ъглите и радиуса на кръга, а след това ще бъде страхотно формула. на която можете лесно да се идентифицират и страни на триъгълника, а след това намери своето място.
5. Интересен случай, когато имаме само координатите на върховете на триъгълник в равнината. Тук, разбира се, можете да намерите на дължината на всяка страна (или стойността на ъгъл) и след това се изчислява площта на триъгълник. Но това ще бъде по-лесно опция, просто напишете детерминантата на трите измерения, в който всеки ред първите два елемента - координатите на един връх и третия модул. След това половината от абсолютната стойност на детерминантата ще бъде зоната на триъгълника.
6. Не по-малко интересен е и пространствено случай на същия проблем. За да го решим, ние първо трябва да намерим координатите на двете страни (вектори) на триъгълника, които излизат от един връх. И тогава, изчисли абсолютната стойност на половината напречно продукт от тези страни.
7. Накрая, последният случай е същият като предишния, само ако са дадени координатите на векторите, те не трябва да се търси. За да се изчисли площта на триъгълник, който се намира върху тях, просто трябва да намерите половината от абсолютната стойност на вектор продукт.

Допълнително съдържание:

Сподели с приятели: