Рекурсия в Pascal, рекурсивни функции и процедури

Ако тялото на функцията отговаря на предизвикателството на този много функции. то това е рекурсия.

Рекурсивно в Pascal може да има и двете функции и процедури.

В действителност, рекурсия може да бъде безкраен. Но, както при всеки друг алгоритъм, той трябва да се върне в резултат след определен определен брой операции.

Затова е важно: На всяка стъпка на процедура или функция на тялото рекурсивния непременно промяна в параметрите на функцията, или наличието на условия, в които вече се не няма да доведе!

Помислете за един прост пример за използване на рекурсивни процедура:

Пример: номера печат последователност в ob.patno ред с помощта на рекурсивни процедура повикване. nappimep:
ред (5) = 5 4 3 2 1
От състоянието на проблема е ясно, че състоянието на завършване на рекурсия е самата аргумент функция, която трябва да се намали с един до е> = 1.

процедура ред (п: число); започва, когато п> = 1 тогава започва записване (п '); ред (п-1) край; приключи; започне ред (10); край.

А сега да разгледаме един по-сложен пример за използване на рекурсия в Паскал.

Пример: Добави рекурсивен процедура, която показва номера минута като реални числа параметри в обратен ред.

Например: ако премина функцията включително 3078. крайна сметка трябва да върне 8703
Използвайте мод и Разделение операции

процедура обратната (п: число); започнете запис (п мод 10); ако (п Разделения 10) <> 0 след това обратно (п Разделения 10) край; започнем writeln; обратно (3078); край.

Рекурсия: печат последователност използване рекурсия:
25,23,21,19,17 ... 0

Сега нека видим как рекурсията се използва при изчисляване на факториел в Паскал.

Пример: Извършване на рекурсивни функции за изчисляване на факториел

Съвет:
2! = 2 * 1 = 2
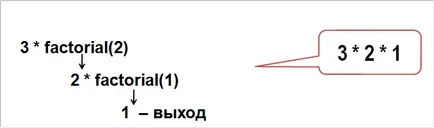
3! = 3 * 2 * 1 = 6
Се получи формула с! = A * ((а-1)!)

Var х: цяло число; Всъщност функция (А: число): цяло число; започне, ако (а<=1) then a:=1 else a:=a*(fact(a-1)); fact:=a; end; begin writeln('Число?'); readln(x); writeln(fact(x)); end.

Рекурсия: Напишете рекурсивна функция sumTo (н). че за даден п изчислява сумата на числата от 1 до п. например:
sumTo (1) = 1
sumTo (2) = 2 + 1 = 3
sumTo (3) = 3 + 2 + 1 = 6
.

Рекурсия. Напишете рекурсивна функция за определяне на степента.

Var х, у: цяло число; функция stepen (а, б: число): цяло число; Var. започне. приключи; започнем writeln ( "номер"); readln (х); writeln ( "степен"); readln (у); writeln (stepen (х, у)); край.

Рекурсия: Необходимо е да се симулира работата на за цикъл. На всеки път, когато думата "здравей" и стойността на брояча. За да направите това, използвайте променлива брояч стъпка, за да се реализира в рамките на параметъра на процедура. Вторият вариант - общият брой на стъпки (брой на повторения на цикъла).

Рекурсия: Намерете GCD от Евклид. Използвайте рекурсивни процедура.

За номера 3430 и 1365:

остатък от участък 3430-1365

3,430 мод 1365 = 700

остатъкът не е нула, да се повтори същото действие, замествайки за първи брой секунди, и вместо втория - остатъкът

1,365 мод 700 = 665

остатък и нула, така друга разделителна

700 мод 665 = 35

остатък и нула, така друга разделителна

Рекурсия: Отпечатване на първите 10 числа на Фибоначи (до 21), като се използва рекурсивен процес с два параметъра.
Резултатът трябва да бъде: 1 2 3 5 8 13 21 34 55 89
Пълна код: