разполага изследвания на изпъкналостите и инфлексия точки - studopediya

График диференцируема изпъкнала функция се нарича определяне на интервали. ако е на всеки от своята допирателна в този интервал (Фигура 13).

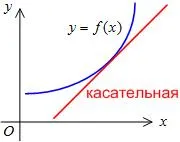
График диференцируема изпъкнала функция се извиква от интервал. ако е разположен по-ниско от някоя от нейните допирателна в този интервал (Фигура 14).

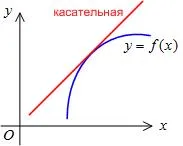
непрекъсната функция точка диаграма. разделяне на части от различни изпъкналост се нарича инфлексна точка.

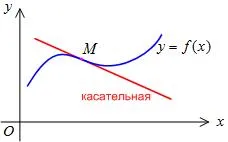
Интервалите са изпъкнали нагоре и надолу чрез следната теорема.

Теорема 1. Ако функцията има отрицателно втори производно във всички точки на интервала, е това. графиката на функцията на този интервал е изпъкнала нагоре. Ако всички точки на интервала, графиката на функцията е изпъкнала надолу.

За да намерите точките на огъване на функцията, ние използваме следната теорема.

Теорема 2. достатъчно условие за точка на инфлексия. Ако втората производна на функцията при преминаване през точка. където вторият производно е равно на нула или не съществува, промяна знак, точката на графиката с абсцисата е инфлексната точка.

Пример. Проучване за изпъкналост и точки на инфлексия на функциите на графиката.

Втората производна съществува на цялата реална ос. Намерете място, където тя е равна на нула :.

Когато стигнем. когато имаме. следователно интервал функция графиката е изпъкнала нагоре

графиката интервал е изпъкнала надолу, така че точката на абсцисата е инфлексната точка.

Въпрос. Колко инфлексна точки е графиката на?