Разчитайте на концепцията

Равнинни графики. Формула на Ойлер.

Да разгледаме изображение графика G. Фигура 34 изобразява графика G, някои ръбове на повторното пресичат. На Фигура 35, една и съща графика G е представен така, че нейните ръбове не се припокриват.
Графиката на фигура 40 е плоска представяне на графиката на фигура 39.

ФИГУРА 39 Фиг. 40
Графика G е равнинна, ако може да бъде изготвен в плоска равнина, така че няма две от ребрата му нямаше други точки общо, освен тяхната обща връх.
Примери за планарни графики са прости цикли, дървета, горски.
Както характеристиките на плосък представяне на графиката TSB-понятието лице.
Edge в жилищна представяне на графика G е част от равнина, ограничена от прост цикъл и не съдържа в други цикли.
Както лицата могат да се считат за част от позицията на самолетни състезания "извън" плоската представяне на графиката; то се ограничава до "вътре" прост цикъл и не съдържа други цикли. Тази част от равнината се нарича "безкраен" лице.

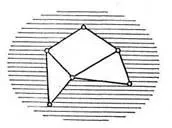
Фиг. 41
На Фигура 41 част от безкрайни лицата сенчести.
Дърво и дървен материал има един аспект на безкрайността.

Фиг. 42
Задача 7.1. На Фигура 42 планарна представяне на графика G. му даде ръба.
Отговор: (1, 7, 4, 1), (1, 3, 2, 4, 1), (1, 2, 3, 1), (2, 6, 5, 4, 2), (1, 2 , 6, 5, 4, 7, 1).
Защо част-PLO равнина, ограничена от прост цикъл (1, 2, 4, 1) не е etsya ръб?
Тъй като обхваща цикъл (1, 2, 3, 1).
Задача 7.2.

Фиг. 43
Какви са всички аспекти на графиката.
Отговор: (1, 2, 3, 4), (1, 2, 3, 4, 5, 1).
Защо е част от равнина, ограничена от прост цикъл (1, 2, 3, 4, 5, 1), е лицето?
Тъй като ръб (4, 5), разположен във вътрешността на лицето не представлява линия.
Задача 7.3.

Фиг. 44
Е част от равнината, zashtri Хов на Фигура 44 ръба?
Отговор: Това не е, защото не е човекоядец-nichena вътре прост цикъл.
Задача 7.1.
Община решава да построи във всеки квартал на града, като 155
кръстовища и улични сегменти 260 между кръстовища, супермаркет.
Колко ще бъде построен супермаркети?
Решение.
карта на града може да се счита планарни графика Г, в която пресечните точки са възли и улични сегменти - ребра.
Планарни графика, показана на Фиг. 45 има три аспекта, където фасетни 1 - извън и лицата 2 и 3 - вътрешните.

Фигура 45
Теорема 10. Формула на Ойлер. За всеки свързан планарна уравнение графика е вярно: п-М + е = 2, броят gden- vershinm- брой ръбове, AF-номер на графиката ръбове.
Доказателство.
Подграф на G, съдържащ всички върховете на графиката се нарича обхващаща. Ако ostavny подграф е дърво, то се нарича обхваща дърво.
Да разгледаме обхваща дърво Tgrafa Г. Ясно е, че в графика Timeet н върховете и една с лице (външен). Тъй като T - дърво, броят на ръбове е равно на Т (п-1). Ето защо, за граф Tdokazyvaemaya формула е вярно. Сега ще поред, но за да се добавят липсващите Т ръбовете на Г. Когато всеки допълнение броят на върховете внезапни проверки и броя на ръбове и е с изложение увеличения на единица-nitsu. Това означава, че формулата ще бъде доказано вярно за всяка графика, получена чрез прибавяне на операциите на ребра, и, следователно, за първоначалното графиката. Това доказва теоремата.
Тъй като квартали на града съответстват на вътрешните повърхности на равнинен граф G, ние откриваме, броят на лицата по формула на Ойлер. Графика G има 155 върхове и 260 ръбове. Броят на лицата в него: F = m - п + 2 = 260-155 + 2 = 107.
В града, за да се изгради 106 супермаркети.
Задача 7.2.
Печатната платка е плоча от изолационен материал, в който специално произведени гнезда монтирани електронни инструменти. Както проводниците, свързващи тези устройства са бомбардирани метални парчета. Тъй като проводниците не са изолирани, пистата не трябва да се преминава. EC-, ако тя може да се случи, че една от песните се прехвърлят към друг сто Рон дъската. Дизайнер Иванов излезе с добра схема на печатна платка, която се състои от 12 устройства и 32 тел, свържете-ING тях. Възможно ли е да се направи такава такса, така че всички кабели са разположени от едната страна?
Решение.
PCB верига могат да бъдат представени като графика, чиито върхове ще представлява автобусни устройства и ръбовете - проводници свързването им. Решение на проблема се свежда до отговора на въпроса: Ще G графиката, изобразяващи инженерът на Иванов плосък?
Нека докажем следната връзка: Твърдение 3: за свързаното с плосък дроб-фа, soderzhaschegonvershin imreber, за Н. 3 изпълнен неравенство stvom. 3n- 6.
Доказателство. Нека G1, G2, ..., Ff- ръба на G графиката, а m1, m2. mf- се ограничава броя на ръбовете, респективно, всяко лице. Намерете сумата S = m1 + m2 +. + Mf.
От всяка страна на графиката, ограничена от поне три ребра, на 3f. С. От друга страна, всеки ръб принадлежи или две лица или едната страна, т.е. в размер на S се взема предвид два пъти или един. Следователно S. 2m. Ние трябва да 3е. 2м. На следващо място, ние използваме формулата на Ойлер:
F = М - N + 2,
3f = 3m - 3N + 6
Два метра? 3м - 3N + 6,
м. 3N - 6.
За п = 3neravenstvo проверява директно.
Неравенството е доказано.
За графиката G, описващ инженер в Иванова, п = 12, m = 32, и по-горе неравенството не е изпълнено.
Затова GNE графика е плоска и да направи едностранно такса nyuyu невъзможно.
Задача 7.3.
Инженер Иванов (см. Предишни проблем) подобрява нейната цена. Сега тя има устройства 9 и 17 от проводниците (виж платка. Фиг. 46). Възможно ли е да се направи на борда, така че всички проводници време бюргери от едната страна?

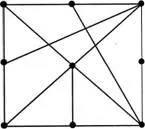
Фигура 46.
Решение.
Предполагаме платка графика Ж. неравенство м. 3N - 6 не може да отговори дали графика G плоски 17. * 3 9 - 6 = 21.
Да разгледаме подграф на G, смели линии на фигура 47.

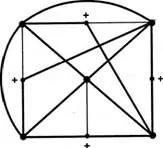
Фиг. 47
Това подграф могат да бъдат получени от пълната графиката с пет върха (С5) поставяне върху някои-ryh ребрата допълнителни върхове. (Фигура K5vydeleny върхове и допълнителни пикове са обозначени знак "+"). Intro-на допълнителни пикове не може да конвертира непланарна графика K5 в апартамента. Следователно, графиката G, чиито подграф е с неравнинна графика е непланарни. Това означава, че за производството на една страна на дъската невъзможно.
Известен теорема, описваща структурата на планарни графики. Ние разделят някои от краищата на графики и K3,3 K5novymi върховете (вж. Фиг. 48). Получените графиките ще бъдат наричани съответно видове графики K3,3 и К5.

Теорема 11.TeoremaPontryagina-Kuratowski (1927,1930грама). Графиката е плоска, ако и само ако той не съдържа видове подграфи K3,3 или K5.