QS с очаквания (опашка)

Като показатели за изпълнение QS с очакване, освен вече известните характеристики - абсолютно и относително трафик, вероятността за неуспех, средният брой на заетите канали към (за система за многоканален), също да се има предвид следното:

1) - средният брой на поръчките в системата;

2) - средно време на престой на заявлението в системата;

3) - среден брой на искания в опашка (дължина опашка);

4) - средното време, прекарано в етапа на кандидатстване;

5) - вероятността, че каналът е зает (канал капацитет степен).

Single-канална система с неограничен опашка

Налице е един канал QS с опашка, на която няма ограничения (или дължината на опашката за изчакване не). Промени приложения, получени от СК е с интензивност, както и потока поддръжка - интензивност. Необходимо е да се намери граница вероятността за условията и показателите за изпълнение SMO.

Системата може да бъде в една от състояния в зависимост от броя на структурите на QS: - каналът е свободен; - канал е зает (служи приложение), не опашка; - каналът е зает, една молба се нарежда на опашка; - каналът е зает, искания са на опашката и т.н.

Брой SMO състояние е показано на фиг. 8.

Този процес на раждане и смърт, но с безкраен брой състояния, в които потока на заявките е равна на интензивността и тече поддръжка процент.

Преди да напишете с формулировка пределни вероятности, трябва да сте сигурни в тяхното съществуване, защото, когато времето всичко може да се увеличи за неопределено време. Доказа, че ако, т.е. средният брой на входящите заявки е по-малко от средния брой на обслужвани искания (за единица време), съществуват пределните вероятностите. Ако, от всички се увеличава до безкрайност.

За определяне на пределни вероятностите членки използват формулите (16), (17) за раждането и процеса смърт (тук ние приемаме, известна липса на взискателност, както по-рано, тези формули са били получени за случая с краен брой състояния на системата). получаваме:

Пример 8. порт има поставка за разтоварване на кораби. Скоростта на потока е 0.4 съдове (кораби на ден). Средното време за разтоварване на кораб, е на 2 дни. Предполага се, че на опашката може да бъде от неограничена дължина. Намери показатели за изпълнение котвена стоянка, както и вероятността, че очакваното освобождаване от отговорност не е повече от 2 съдове.

Решение. Ние имаме. Тъй като, след което включете разтоварят не може да се увеличи до безкрайност и да ограничи вероятността от там. Намерете ги.

Вероятността, че на кея е свободен да (33), както и вероятността, че той е зает. С формула (34), вероятността, че леглото са 1, 2, 3 на съда (т.е., в очакване разтоварване 0, 1, 2 съдове) са равни

Вероятността, че очакваното освобождаване от отговорност е не повече от 2 кораб

Чрез формула (40), средният брой на корабите, чакащи разтоварване, средното време за изчакване на освобождаване от отговорност по формулата (42) (през нощта).

Съгласно формула (36), средният брой на плавателни съдове при престоя (дни) (или по-просто (37) (ден) и средното време на престой на кораба на кея с формула (41) (дни).

Очевидно е, че ефективността на разтоварването на корабите е ниска. За да се подобри, че е необходимо да се намали средното време на разтоварване на кораба или да увеличи броя на корабни места.

QS Многоканални с неограничен опашка

Помислете за проблема. Има една п-канал QS с неограничен опашка. Промени приложения, получени от СК е с интензивност, както и потока поддръжка - интензивност. Необходимо е да се намери най-лимит на вероятностите държавни QS и изпълнение на неговата ефективност.

Системата може да бъде в една от страните номерирани според броя на субекти в ООП: - системата все още няма оферти (всички канали са свободни); - един канал е зает, на останалата свободна; - два канала са заети, а други са свободни; - канал е зает, а други са свободни; - всички канали са заети (без опашката); - заети всички канали в опашката едно приложение; - всички канали са заети, заповеди, чакащи на опашките, и т.н.

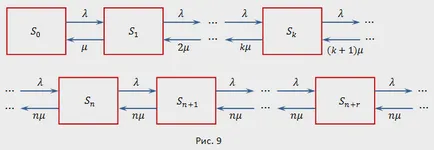
статус Брой система е показана на Фиг. 9. Трябва да отбележим, че за разлика от поддържането поток предишната интензивност QS (прехвърля на системата от едно състояние в друго, нали) не остава постоянна, но тъй като броят на приложенията в СК се увеличава от 0 до степента, че са били съответно на броя на каналите на услуги се увеличава. Ако броят на приложенията в СК по-голяма от скоростта на потока се съхранява услугата равни.

Тя може да се докаже, че са налице ограничаване на вероятностите. Ако, от всички се увеличава до безкрайност. Използване на формули (16) и (17) за процеса на раждане и смърт, може да се получи по следната формула за пределните вероятностите на състояния п-канал QS с неограничен опашка

Средното време за пребиваване в опашката за кандидатстване, както и средното време за пребиваване в системата за кандидатстване, както и преди, са дадени от Little (42) и (41).

Забележка. За QS с неограничен опашка по всяко приложение, което влезе, тя ще бъде взети под внимание, т.е. вероятността за провал, относителната широчина на честотната лента и честотна лента е равен на абсолютен интензивността на входящия поток на искания, т.е. ,

Пример 9 в супермаркета, за да се изчисли възел влезе в потока на клиенти на интензивността на хора. на час. Средната продължителност на услугата контролер на приказки един купувач мин. дефинират:

а. Минималният брой на касиери, контролери, които не се редят на опашки ще расте до безкрайност, и подходящи характеристики за поддръжка на адрес.

инча Вероятността, че линията няма да е повече от три купувачи.

Решение. а. От състоянието (1 / ч) (1 / мин.). С формула (24). Опашка няма да расте до безкрайност, при условие че с \ р = 2, \! 7 "SRC =" http://bourabai.ru/cm/waiting_sys/mathtex(82).gif ">. По този начин минималният брой контролери-касиери.

Ние считаме, характеристиките на обслужването в общата референтна рамка.

Вероятността, че възловата точка не изчисление купувачи, от формула (45)

т.е. средно от 2.5% на касите на времеви контролери ще бъде празен.

Вероятността, че изчисляването на възел ще се включи (48)

Средният брой на клиентите на опашката, от (50)

Средното време, за да чака на опашка и си купят билети, така или иначе, съответно (в съответствие с формули (42) и (41)):

Според втория вариант имаме две QS един канал (две специализиран прозорец); за всеки входящ поток на искания с интензивност. Както и преди, са налице ограничаване на вероятностите. Според формули (40) и (36), (42), (41)

Така че, на втория вариант и увеличената дължина на опашката, а средното време за изчакване в него, и като цяло, за закупуване на билети. Тази разлика се обяснява с факта, че в първия вариант (два канала SMO) е по-малък от средния процент от време, който бездейства една от двете преброителите, ако той не е зает обслужване на пътник купува билет до точката, той може да направи за обслужване на пътници, който закупи билет до точка, както и обратното , Във второ изпълнение, няма такава взаимозаменяемост.

Тя може да се види, че средното време се е увеличил повече от 2 пъти за закупуване на билети за втория вариант. Това значително увеличение се дължи на факта, че общата референтна рамка работи при максимален капацитет: само леко да се увеличи средното време за обслужване, т.е. намалява и надвишава 1, т.е. всичко да започне да расте неограничено време.

б. Над бе установено, че в съответствие с първото изпълнение на билети при средна време услуга един пътник (мин) средно време за покупка на количество билети (мин). По предположение за второто изпълнение на продажба, или като се вземат предвид (36) и (41).

Ако приемем, че ние получаваме където намери или (м).

Така, средното време за закупуване на второто изпълнение на билети намали, ако средното време за обслужване на пътник намалява с повече от 0.17 m, или повече от 8,5%.

QS с ограничена Queuing

QS с ограничен опашка различни от тези по-горе, само с това, че броят на исканията на опашката е ограничен (не може да надвишава определен предварително зададен). Ако новото приложение идва в момент, когато всички места са заети в опашката, той напуска SMO необслужваните, т.е. е отказано.

Очевидно е, че за изчисляването на ограничаване вероятности на състоянията и ефективността на такива SMO може да се използва същия подход както по-горе, с тази разлика, които обобщават не трябва безкраен прогресия (както направихме в получаването на формула (33)), и на финала , Съответните формули са показани в таблица. 3.

Средното време на престой в опашката, и прилагането на системата, както е определен от формула Малката (44) и (43).

Пример 11 Пример 8 Чрез търсене хипотеза показатели за изпълнение, кей. Известно е, че входящите кораб напуска дока (не разтоварват), ако опашката за разтоварване е на стойност повече от 3 съдове.

Решение. При условие. Ние използваме формулите, дадени във втората колона на таблица. 3.

Вероятността, че кея е свободен,

Вероятността входящо кораб тръгва на подсъдимата скамейка, без разтоварване:

Среден брой плавателни съдове при престоя и средното време, прекарано на кораба на кея (41):

QS с ограничен латентност

На практика често QS с така наречените "нетърпеливи" приложения. Тези заявления могат да оставят на опашката, ако времето за чакане превишава определена сума. По-специално, този вид приложение се осъществява в различни технологични системи, които да забавят началото на услуги може да доведе до загуба на качество на продуктите, системи за оперативно управление, когато спешни съобщения, за да загубят стойността (или смисъла), ако те не правят услуга за определен време.

В такива системи, се приема, прост математически модел, че приложението може да бъде на опашката за произволно време, разпределени експоненциално с определен параметър, т.е. Може условно може да се предположи, че всяко приложение, за да стоят в линия за обслужване, може да напусне системата с интензивност.

Подходящи показатели за изпълнение QS с ограничен период от време са получени въз основа на резултатите, получени в процеса на раждане и смърт.

В заключение, ние отбелязваме, че на практика често се срещат затворен за поддръжка на системата. в който входящ поток от заявки по същество зависи от състоянието на Обсерваторията на единния пазар. Като пример, ситуация, в която ремонтни съоръжения от експлоатация на полето на някои от колите: ясно е, че колкото по-машината е в състояние на ремонт, толкова по-малко продължава да се използва и по-ниска е интензивността на потока от нови участници на ремонта на машините. За затворен QS характеристика е ограничен брой приложения източници всеки източник "блокиран" по време на обслужване на неговото прилагане (т.е. тя не издава нови искания). В такива системи, краен брой състояния QS пределната вероятност ще съществува за всяка стойност на приложения и услуги за дебит. Те може да се изчисли, ако се върне към процеса на раждане и смърт.

Знаете ли, че времето мащаб - число, което определя продължителността на симулационен модел на една единица от време, преизчислени в секунда, в реално време, Астрономически секунди, когато модела.

Новини
Knights етер теория