пъзел Макарова

Светът е подредена така, че нещата в него могат да живеят по-дълго, отколкото хората, които имат различни имена в различни периоди и в различни страни, ние дори могат да играят игри Симпсън. Играчката, която можете да видите на фигурата, позната у нас като "пъзел адмирал Макаров". В други страни, то има и други имена, от които най-често - ". Проклета възел" "кръст на дявола" и

Това устройство е свързано от 6 квадратни решетки. Лентите имат вдлъбнатини, които правят възможно и пропускателни барове в центъра на възела. Един от баровете още няма вдлъбнатини, той е поставен в последния възел, както и по време на демонтажа е отстранен първи.

Сега пъзела, можете да си купите в магазина, но това е хубаво да го направя на ръка. Най-подходящия размер барове за импровизиран строителство: 6h2h2 см.

Разнообразието от кървави възела

Преди началото на века, няколко стотин години от съществуването си играчки в Китай, Монголия, Индия и е изобретен повече от сто варианти на пъзела, която се различава по конфигурацията на прорезите в баровете. Но най-популярни са два варианта. Показан на фигура 1 е решен много лесно, просто и да го направи. Тя е тази структура, използвана в древен индийски ковчег. Пъзел, съставен от баровете на фигура 2, която се нарича "възел Дяволският". Както можете да си представите, името тя получава за трудни решения.

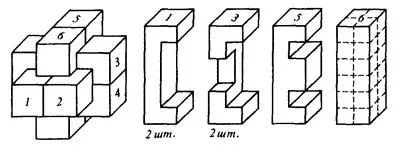
Фиг. 1 Най-простият вариант на пъзела "кървав възел"

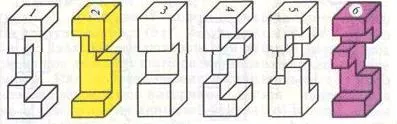
В Европа, където, тъй като в края на миналия век, на "Knot Дяволското" все повече набира популярност, ентусиасти започнали да мислим и правим комплекти от барове с различни конфигурации на изрези. Един от най-успешните комплект произвежда 159 пъзели и се състои от 20 атм 18 вида. Докато всички възли са неразличими на външен вид, те са съвсем различен начин поставя вътре.

Фиг. 2 "Golovlomka адмирал Макаров"

Настойчиво всички в това търсене е холандски професор по математика Ван Де Боер, който със собствените си ръце направи колекция от няколкостотин барове и съставени таблици, които показват как да се съберат 2906 опции възли.

Това беше през 60-те години, а през 1978 г. на американския математик Бил Кътлър пише програма за компютър и груба сила са установили, че има 119,979 опции пъзели на 6 елементи, различни комбинации от издатини в баровете, както и настаняването барове, с уговорката, че не кухини във вътрешността на възел.

Изненадващо голям брой за такава малка играчка! Следователно, за да се реши проблема и се нуждае от компютър.

Тъй като компютърът решите пъзела?

Разбира се, не като човек, но не и по някакъв магически начин. Компютър решава пъзели (и други обекти) на програмата, програмистите пишат програми. Напиши, както им е удобно, но така че да е ясно и компютри. Как може един компютър манипулира дървени барове?

Ние изхождаме от факта, че ние разполагаме с набор от 369 бара, които се различават едни от други конфигурации на издатини (първата група от определени Ван Де Боер). Компютърът трябва да въведете описание на тези барове. Минималната вдлъбнатината (или издатината) в бара - един куб с ръб на дебелина 0,5 бар. Нека го наречем един единствен куб. Като цяло, такива лента 24 съдържа куб (Фигура 1). Компютрите за всеки бар се поставят "малък" масив от 6h2h2 = 24 числа. Бар с прорези определена последователност от 0 и 1 в "малък" масива: 0 съответства издълбани куб, 1 - цяло. Всеки един от "малките" масиви има свой собствен номер (1-369). Всеки от тях може да се причисли към друг номер от 1 до 6, което съответства на положението на лентата в пъзела.

Сега е ред пъзела. Представете си, че да пасне във вътрешността на измервателната куб 8h8h8. Компютърът, който съответства на куба на "голям" набор от 8h8h8 = 512-клетките. Сложи малко бар вътре в куба - това означава да попълнят съответната клетка "голям" набор от числа е равен на броя на бара.

Сравнявайки 6 "малки" масиви и основно, компютър (т.е.. Д. програма), като го допълва, заедно с 6 бара. Според резултатите от добавянето на номера го определя колко и какви "празен", "пълни" и "пренаселени" клетки, образувани в основния масив. "Blank" клетка съответства на празното пространство вътре в пъзела ", изпълнен" - съответстващи на издатините в баровете и "пренаселено" - опит да се комбинират заедно две единични куб, който, разбира се, е забранено. Такова сравнение е направено на няколко пъти, а не само с различни барове, но и с оглед на своите завои, местата, които заемат в "кръста", и така нататък. Н.

В резултат на това, изберете тези опции, които не са празни и пренаселени килии. За да се реши този проблем ще бъде достатъчно "големи" размери масив 6h6h6 клетки. Оказва се обаче, че има комбинации от барове, цялостно запълване на вътрешния обем на пъзела, но те не трябва да се разглобява. Ето защо, програмата трябва да е в състояние да провери възела относно възможността за демонтаж. За тази цел Кътлър и взе масив 8h8h8, макар и размерът му може да не е достатъчна, за да тествате всички случаи.

Той е пълен с информация за пъзели вариант. В рамките на програмата на масива се опитва да "се движат" решетките, т. Е. премества в "голям" размер на масива на лентата 2h2h6 клетки. Заместването се извършва в една клетка във всяка от 6 посока, успоредна на осите на пъзела. Резултатите от шест опити, които не се образува "претъпкани" клетки се съхраняват като изходно положение за следните опити Sixes. дърво резултат е изработена от всички възможни движения, докато всеки блок не е изцяло от основното тяло или след всички опити да остане "пренаселени" клетки, това е тази, която не може да се разглоби.

Това е са получени чрез компютърна 119,979 опции "Възел Дяволското", в това число не 108, както древните, както и версията с 1 цялата 6402, без съкращения бар.

Имайте предвид, че Кътлър се отказа от общ проблем - когато един възел съдържа както вътрешни кухини. В този случай, броят на възли от 6 бара, се увеличава значително и изчерпателно търсене необходимо да се намери на изпълними решения, не е реалистично, дори и за съвременния компютър. Но както ще видим сега, най-интересните и предизвикателни пъзели го намерят в най-общия случай - разглобяване пъзела след което можете да направите е далеч от тривиално.

Поради наличието на кухини, че е възможно да се движи последователно няколко бара, преди да може да се отдели напълно всеки бар. Преместването на бара освободи някои барове, позволява движението на следващата лента, и едновременно с това се занимава останалите барове.

Колкото повече, което трябва да направите, манипулации по време на демонтажа, толкова по-интересно и по-трудно версия на пъзела. Слотовете в баровете са подредени така хитро, че търсенето на решения припомня скитащи тъмния лабиринт, в който през цялото време се сблъскват с нещо на стената, а след това без изход. Този тип възел е несъмнено заслужава ново име; ние ще го наричаме "supernode". Supernodes мярка сложност се нарича броя на движението на отделни ленти, които трябва да бъдат направени преди първия елемент се отделя от пъзела.

Създавайте чертежи такива трудни пъзели като supernodes, а не за да разкрие тайните им ще бъдат твърде жестоки дори да ценителите на пъзели. Ние ще дадем решение supernodes в компактен, правоъгълна форма.

Преди разглобяване приемане пъзел и се ориентират така, че да съответства на изготвяне номера 1. демонтаж последователност се записват като комбинация от цифри и букви. Числата представляват много барове, писма - посока на движение, в съответствие с които е показано на фигури 3 и 4, координира система. Резултат над движение в отрицателна посока на оста на координатната. Една стъпка - е движението на бара 1/2 от неговата ширина. Когато лентата се придвижва две стъпки едновременно, неговото движение се записва в скоби с експонентата 2. Когато се премества няколко части, които са ангажирани с друг, те сключват числа п скоби, например (1, 3, 6) х. Разделяне бар на пъзела е белязана от вертикална стрелка.

Сега дайте примери за най-добри supernodes.

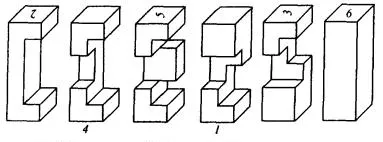
Пъзел W. Кътлър ( "трън Бил")

Тя се състои от части 1, 2, 3, 4, 5, 6, както е показано на фигура 3. Също така даден алгоритъм разтвор. Интересното е, че в списание "Scientific American" (1985 г., брой 10) е различна версия на пъзела и се съобщава, че "трън законопроекта" има уникално решение. Разликата между изпълненията - само един бар: 2 и 2 подробно на фигура 3.

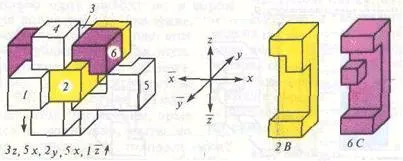
Фиг. 3 "Барб Бил", проектирана от компютър.

Поради факта, че част 2 съдържа по-малко, отколкото съкращения детайла 2, поставете го в "трън в очите на Бил" на определен алгоритъм на Фигура 3 не е възможно. Би могло да се предположи, че пъзела на "Scientific American" ще се по някакъв друг начин.

Ако това е така и ние ще го събира, тогава, след това можем да се замени т.2 т.2, тъй като последната заема по-малък обем от 2 V. В резултат на това ние получаваме второто решение на пъзел. Но "трън законопроекта" има уникално решение, както и от нашите противоречия може да се направи само един извод: втората версия от грешка на фигурата.

Filippa Dyubua пъзел (фиг. 4)

Той се разтваря в 7 се движи до следния алгоритъм: (6z) ^ 2, 3x. 1Z, 4x, 2x, 2г, 2г. Ха цифра показва местоположението на части за демонтаж на B кобила. Като се започне от това положение, като се използва обратен ред на алгоритъма и да промени посоката на движение в обратното, можете да се съберат пъзела.

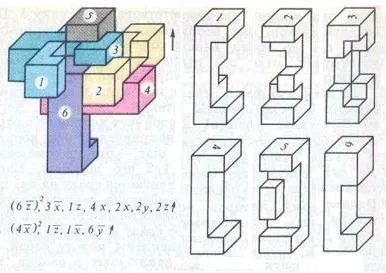
Фиг. 4 supernode F. Всяка трудност 7

Три supernodes Г. Vakarelova.

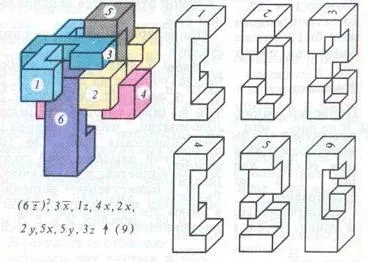
Фиг. 5 supernode от 9 D.Vakarelova

Първият от неговите пъзели (Фигура 5.) - това е подобрена версия на пъзела Дюбоа, той има проблем с 9. Това supernode повече от други като лабиринт, като при демонтажа възникват лъжливи ходове Вълнуващи мъртвите зони. Пример за такава безизходица - Sx ходове, 1Z рано демонтаж. Правилното решение е:
(6z) ^ 2, Sx, 1щ, 4х, 2x, 2y, 5х, 5Y, 3Z?.

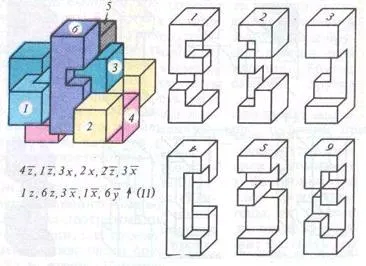
Фиг. 6 supernode D. Vakarelova от 11

(. Фигура 6) втори пъзела Vakarelova D. се решава чрез формулата:
4г, 1Z, Sx, 2x, 2z, Sx, 1Z, 6z, Sx, 1x, 3z?

и има сложност 11. Забележително е, че на бара 3 в третия завой прави Sx стъпка и обратно (Sx) се връща на шесто скоростта; и 1 бар във втория етап, като движите 1Z и 7 ход също се завръща инсулт.

Фиг. 7 supernode D. Vakarelova от 12

Третият пъзела (Фигура 7.) - един от най-трудните. Нейното решение:
4Z, 1щ, Sx, 2x, 2Z, Sx, 6z, 1щ, (1,3,6) х, 5Y?

до седмия ход повтаря предишния пъзела, а след това, за да отидат 9 настъпва напълно нова ситуация: изведнъж всички барове спрат да се движат! И тогава ще трябва да се премести веднага да се отгатне 3 бара (1, 3, 6), а ако това движение се разглежда като продължение на 3 завои, а след това сложността на пъзела ще бъде равен на 12.

Изберете подходяща бележка оценка: