Продължава фракции
Глава I. ПРАВО краен продължение фракция
§1. Представянето на рационални числа от продължиха фракции
§2. Съответните фракции. Техните свойства.
Глава II. Безкрайни продължиха фракции
§ 1. Въвеждане на реални ирационални числа коригира безкрайни верижна дроб
1.1. Разбиване на недвижими ирационално число в правилната безкрайна верижна дроб.
1.2. Конвергенция правилните безкрайни верижна дроб.
1.3. Уникалността на реалното представяне на едно ирационално число коригиране безкрайна верига фракция
§2. Сближаването на действителния брой на рационални дроби с допустимото ограничение знаменател
2.1. оценка за грешка при подмяна на реално число, подходяща фракция.
2.2. Сближаването на действителния брой на съответните фракции
2.3. Дирихле теорема.
2.4. Подходящ за най-добър сближаване на фракцията
§3. Квадратичен ирационалност и периодични продължиха фракции.
§4. Представяне на реални числа от продължиха фракции общ вид.
Целта на моята курсова работа е да се изследва теорията за продължиха фракции. В него се опитате да отворите свойствата на съответните фракции, особено разширяването на реални числа в неправилни дроби, грешките, които възникват в резултат на това разширяване, и прилагането на теорията за продължиха фракции за решаване на някои алгебрични проблеми.
Продължава фракции бяха въведени през 1572 от италианския математик Bombelli. Настоящото обозначението продължиха фракции се намира в италиански математик Cataldi в 1613. Най-големият математик на ХVIII век Леонард Ойлер напред описва теорията на продължиха фракции, повдигна въпроса за използването им за решаване на диференциални уравнения, да ги прилага за разлагането на функцията представлява от безкрайните продукти, като се има предвид значението на тяхното обобщаване.
на теорията на продължиха фракции на работа Ойлер продължава от М. Sofronov (1729-1760), Академик VM Viskovaty (1779-1819), Даниел Бернули (1700-1782) и др. Много от важните резултати от теорията, се дължат на френския математик Лагранж, който е намерил начин на приблизителни решения, използвайки продължиха фракции, диференциални уравнения.
Глава I. Право краен верижна дроб.
§1. Представянето на рационални числа от продължиха фракции.
Един цяло число, което е делител на всеки от числа
, Тя се нарича общ делител на числата. Общ делител на тези числа се нарича най-голямата им общ делител, ако тя се дели на всички числа данни общ делител.
- рационално число, и б> 0. Прилагането а и б Евклид алгоритъм, за да се определи най-големият им общ делител получи крайния системата уравнения:
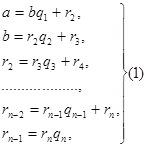
където частичните коефициенти на последователни деления
,
, ...,
наречен елементи на продължава фракция.
алгоритъм на Евклид дава възможност да се намери представителство (или разлагане) на всяко рационално число като верижна дроб. Като елементи на продължава фракция, получена частични коефициенти на последователни деления в системата от уравнения (1), така че елементите на веригата се наричат също удар частични коефициенти. Освен това равенство на (2) показват, че разграждането в продължение фракция е последователно разпределение на превръща в цяло число част и фракционна част.
Последното схващане е по-общо от първия, тъй като тя е приложима за разлагането на верижна дроб е не само рационално, но и всяко реално число.
Разбиване на рационално число
очевидно има краен брой елементи, като алгоритъм последователно deleniyaa МаВ Евклид е ограничен.
Разбираемо е, че всяка конкретна верига фракция е рационално число, т.е. равни на определен брой рационално. Но въпросът не е дали има различни мнения от един и същи рационално число продължи фракция? Оказва се, че там не е, ако той е длъжен да го направи
.
Теорема. Налице е един и само един краен верига фракция, равна на тази рационално число, но с уговорката, че
.
Доказателство: 1) Отбележете, че в случай на повреда на това условие, че представянето е отстранен. В действителност, когато
:
така че идеята може да бъде удължен:
например, (2, 3, 1, 4, 2) = (2, 3, 1, 4, 1, 1).
, и така нататък; Следователно, ние се стигне до следното заключение за взаимното положение на съответните фракции:
повечето от convergents на нечетен ред и по-малко от всички convergents на още ред;
2) нечетен ред подходящи фракции представляват възходящо последователност и дори ред - намаляване (в случая на ирационално
тези последователности са безкрайни), т.е.
(В случай на един рационален
).
-
----
-
---
----
Като се има предвид факта, че
, преминете към по-нататъшно до заключението, че в случай на ирационално
,
, ... форма договаряне последователност, която, както е известно, трябва да имат една обща точка, която е обща рамките на последователността
,
,
Той принадлежи към всички сегменти на последователност,
и съвпада с каза точка, така че
.
Така че, ние имаме следната важният резултат:
безкрайно последователността на convergents
, която възниква от разлагането на ирационалното
, Колебая се за това. Или: ирационално недвижими
равна на границата на неговата последователност подходящи фракции разлагане безкрайно непрекъснато фракция (подбор процес число част).
1.2 сближаването на правилните безкрайни продължение фракции.
Ние сега показват, че конвергентна последователност не само подходящи фракции като безкрайна непрекъснато фракция, което се случва по време на разлагането на ирационално брой
, но всеки безкрайно продължаващата фракция
- произволно избрани положителни числа.
Но за това, ние преразгледа относителното положение на съответните фракции.
За тази цел, помислете по формулата:
които са валидни за всяка безкрайна верижна дроб.
1. Формула (1) показва, че всяка подходяща част от дори поръчва повече от два съседни подходящите фракции, чиято цел е по-малко или повече от него, т.е.
от лявата страна на
,
Този курс работа показва важността на продължиха фракции в математиката.
Те могат да се прилагат успешно към разтвора на неопределени уравнения на форма брадва + = чрез С. Основната трудност при решаване на тези уравнения е да се намери някой от неговото конкретно решение. Така че, с помощта на верижна дроб може да бъде един алгоритъм за намиране на това конкретно решение.
Продължава фракции могат да бъдат приложени по-сложни неопределени уравнения, например, уравнение т.нар Pell е:
(
).
Безкрайни вериги фракции могат да бъдат използвани за решаване на алгебрични уравнения и трансцедентни за бързо изчисляване на стойностите на определени функции.
В момента продължават фракции се използват все по-често в областта на компютърните технологии, тъй като дава възможност за изграждане на ефективни алгоритми за решаване на редица проблеми на компютри.
1. MB BALK, GD BALK. Математика след училище. M, "Образование" 71.
2. AA Buchstab. теория на числата. M "образование" 96.
3. алгебра и теория на числата. Редактирано от Н. Vilenkin, M, "образование" 84.
4. IM Виноградов. Основи на теорията на номера. M, "Наука", 72.
5. AA Кочева. Книга на проблеми в алгебра и теория на числата. M "образование" 84.
6. LY Куликов, AI Moskalenko, АА Fomin. Проблеми по алгебра и теория на числата. M "образование" 93.
7. ES Lyapin, AE Evseev. Алгебра и теория на числата. M "просвета", 74.
8. математическа енциклопедия, том V, M, "съветски енциклопедия", 85.
9. Sh.Kh. Mihelovich. теория на числата. М ", СОУ" 67.